Интегрирование рациональных функций
В предыдущей лекции мы познакомились с основными приемами вычисления неопределенного интеграла. Эти приемы не определяют точно пути, по которому следует идти, чтобы вычислить заданный интеграл, предоставляя многое искусству вычислителя.
Рассмотрим подробнее некоторые важнейшие классы функций и по отношению к их интегралам установим вполне определенный порядок вычислений.
Известны сравнительно немногие классы функций, для которых интегрирование может быть выполнено в конечном виде, т.е. первообразная может быть выражена через элементарные функции. Простейшим из таких классов является класс рациональных функций. Целые рациональные функции интегрируются просто – используя табличные формулы и свойство линейности. Поэтому рассмотрим интегрирование дробно-рациональных функций (рациональных дробей), т.е. функций вида
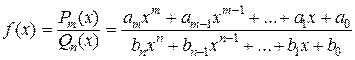 .
.
Из линейной алгебры известно, что всякую рациональную дробь можно разложить на сумму простейших дробей типа
I. 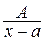 ( А, а – константы) ( А, а – константы)
|
II. 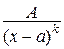 , ( k ³ 2 целое число)
, ( k ³ 2 целое число)
III. 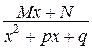 ( М, N, p, q – константы, дискриминант знаменателя меньше нуля)
( М, N, p, q – константы, дискриминант знаменателя меньше нуля)
IV. 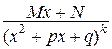 ( k ³ 2 целое, знаменатель не имеет корней)
( k ³ 2 целое, знаменатель не имеет корней)
Интегрирование дробей I – III типов трудностей не представляет. Действительно,
I. 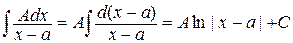 ,
,
II. 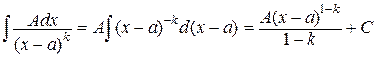 ,
,
III. 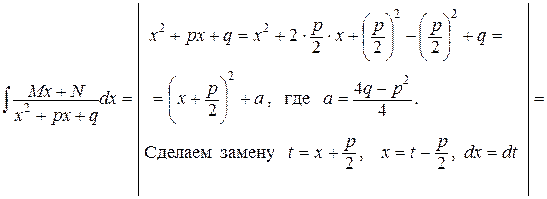
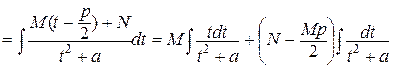 .
.
Таким образом, интегрирование свелось к двум интегралам, один из которых - табличный:
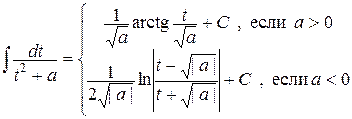 ,
,
а второй легко вычисляется подведением под знак дифференциала:
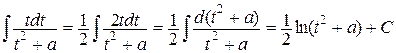 .
.
Интегралы IV типа требуют более сложных вычислений. Но и в этом случае выделение полного квадрата в знаменателе, а затем замена 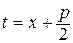 дает возможность упрощения интеграла. В частности, интеграл вида
дает возможность упрощения интеграла. В частности, интеграл вида 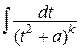 можно вычислить, используя интегрирование по частям, а можно воспользоваться рекуррентными формулами, которые имеются в любом справочнике по высшей математике.
можно вычислить, используя интегрирование по частям, а можно воспользоваться рекуррентными формулами, которые имеются в любом справочнике по высшей математике.
Таким образом, если заданную рациональную дробь разложить в сумму простейших, то интегрирование этой суммы уже не составит особого труда.
Пример 1.
Найти : а) 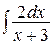 ; б)
; б) 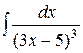 ; в)
; в) 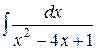 ; г)
; г) 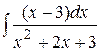
Решение.
а) 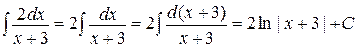 ;
;
б) 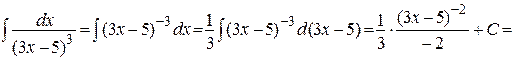
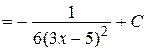 ;
;
в) 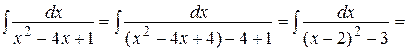
= 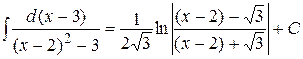 ;
;
г) 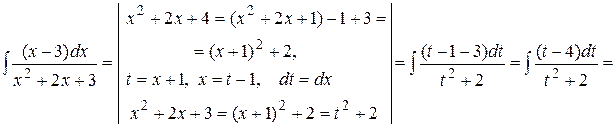
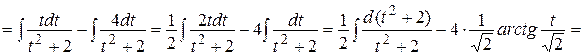
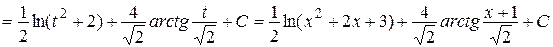 .
.
Пример 2.
Найти 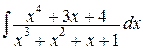
Решение. Подынтегральная функция 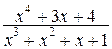 есть неправильная рациональная дробь. Сначала выделим целую часть этой дроби, для чего разделим числитель на знаменатель:
есть неправильная рациональная дробь. Сначала выделим целую часть этой дроби, для чего разделим числитель на знаменатель:
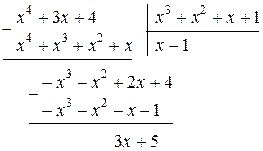 ,
,
тогда 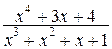 = х – 1 +
= х – 1 + 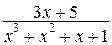 .
.
Рассмотрим правильную дробь 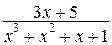 и разложим ее на простейшие:
и разложим ее на простейшие:
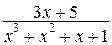 =
= 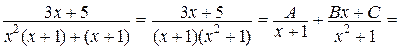
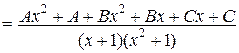 .
.
Сравнивая числители полученной и исходной дробей, находим
 х2 А + В = 0
х2 А + В = 0
х В + С = 3 Þ А = 1, В = –1 , С
св.чл. А + С = 5.
Значит, 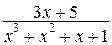 =
= 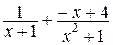 . Тогда, искомый интеграл равен
. Тогда, искомый интеграл равен
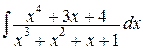 =
= 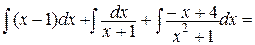
= 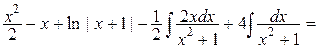
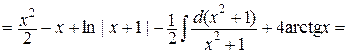
= 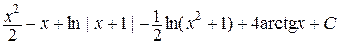 .
.
Дата добавления: 2017-11-21; просмотров: 1015;











