Обобщенная формула Бальмера

для частоты: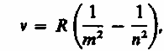

В каждой данной серии постоянное значение, m = 1, 2, 3, 4, 5, 6 (определяет серию), n - принимает целочисленные значения, начиная с числа m +1 (определяет отдельные линии этой серии).

При m = 1 получаем серию Лаймана, при m = 2 - серию Бальмера и т.д. Таким образом, для каждой серии число m = const, а число n меняется. При n = m + 1 длина волны для данной серии имеет наибольшее значение. Это головная линия данной серии спектра - спектральная линия с наибольшей длиной волны из всех линий данной серии. При n= , для данной серии получаем наименьшее значение длины волны λ. Это граничная линия данной серии спектра - коротковолновая граница, к ней примыкает непрерывный спектр.

Обобщенная формула Бальмера (для длины волны):

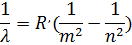
(R’ = 1,1·10⁷ м^-1 -постоянная Ридберга, 1/ λ – волновое число)

Приведенные выше сериальные формулы подобраны эмпирически и долгое время не имели теоретического обоснования, хотя и были подтверждены экспериментально с очень большой точностью. Вид сериальных формул, удивительная повторяемость в них целых чисел, универсальность постоянной Ридберга свидетельствуют о глубоком физическом смысле найденных закономерностей, понять который в рамках классической физики оказалось невозможным.