Виды параллельных контуров и их обобщенная схема

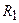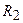Параллельным колебательным контуром называется электрическая цепь, в которой индуктивности и ёмкости расположены в двух параллельно включённых ветвях (рис. 12.1). Сопротивления и учитывают неидеальность реактивных элементов контура. В зависимости от того, как включены индуктивности и ёмкости в ветви контура, различают параллельные контура первого вида (рис. 12.1, а), второго вида (рис. 12.1, б) и третьего вида (рис. 12.1, в).

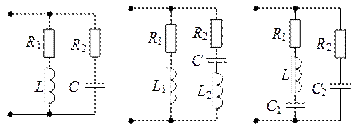
а) б) в)

Рис. 12.1

Указанные виды параллельных колебательных контуров могут быть представлены в виде одно обобщенной схемы замещения (рис. 12.2), которая состоит из двух ветвей с комплексными сопротивлениям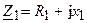и и .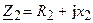

Определим проводимость схемы замещения (рис. 13.2)

,

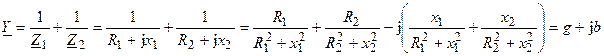где 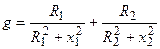, — эквивалентные активная и реактивная составляющие проводимости.

Видно, что активная и реактивная составляющие проводимости параллельного контура любого вида всегда имеют конечное значении на частоте близкой к нулю и на бесконечно большой частоте. Однако на практике этим часто пренебрегают, наибольший интерес представляет частотная область вблизи резонансной частоты, то есть далекая от указанных предельных значениях частоты. Кроме того, практическое применение находят колебательные контура с малыми сопротивлениями потерь, для которых на частотах, близких к резонансной частоте, выполняются следующие условия 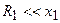, 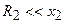и 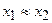, и с учётом которых составляющие проводимости могут быть приближенно записаны в виде:

;

.

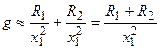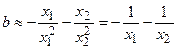В этом случае проводимость цепи (рис. 14.13) определяется следующим приближенным выражением

.

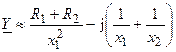Ранее было установлено, что при резонансе токов реактивная составляющие проводимости равна нулю 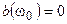, и полная проводимость цепи является вещественной

.

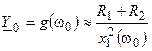Используя условие резонанса токов, составить уравнение

,

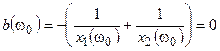которое преобразуется к виду

.

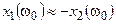Отсюда следует, что в параллельном колебательном контуре с малыми потерями резонанс токов наступает, когда реактивные составляющие сопротивления участков цепи, содержащих емкости и индуктивности, равны по абсолютной величине и противоположны по знаку, что совпадает с условием резонанса напряжений в последовательном колебательном контуре.

С учётом сделанных допущений проанализируем различных виды параллельных колебательных контуров вблизи резонанса.