Виды связанных контуров и их обобщённая схема

Связанными колебательными контурами называется электрическая цепи, состоящая из двух и более колебательных контуров, если возбуждение колебаний в одном из них приводит к возникновению колебаний в других контурах.

Если цепь состоит только из двух контуров, то она называется двухконтурной. Если число контуров больше двух, то цепь называется многоконтурной. Далее будут рассмотрены только двухконтурные цепи, показанные на рис. 13.1.

В зависимости от типа реактивных элементов, с помощью которых осуществляется связь между контурами, различают связанные контуры с индуктивной трансформаторной(рис. 13.1, а), индуктивной автотрансформаторной(рис. 13.1, б), внутренней ёмкостной(рис. 13.1, в)и внешней ёмкостной(рис. 13.1, г)связью. Возможна также комбинированная индуктивно-ёмкостная связь, когда одновременно используются индуктивность 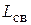и ёмкость связи, но далее она не рассматривается. Контур, к которому подключен источник напряжения, называется первичным, а контур, связанный с первичным, — вторичным.

Рис. 13.1

Связанные колебательные контура (рис. 13.1), могут быть заменены обобщённой схемой (рис. 13.2), в которой сопротивление 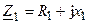, 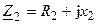— собственные комплексные сопротивления контуров, не учитывающие их взаимное влияние контуров друг на друга, а 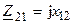— комплексное сопротивление связи, которое имеет реактивный (индуктивный или ёмкостной) характер.

Составим систему уравнений электрического равновесия цепи (рис. 13.2), используя метод контурных токов,

где 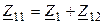и 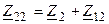— комплексные сопротивления контуров с учётом сопротивления связи, но без учёта взаимного влияния контуров друг на друга.

Из второго уравнения можно ток вторичного контура выразить через ток первичного контура

.

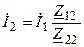Откуда следует, что ток вторичного контура пропорционален току первичного контура.

Решая систему уравнений, находим контурные токи

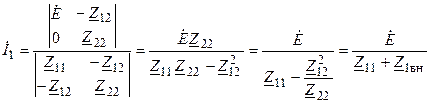; (13.1)

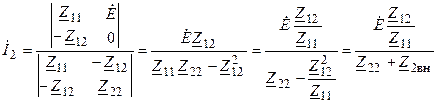, (13.2)

где 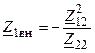— вносимое сопротивление первичного контура, обусловленное влиянием вторичного контура; 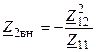— вносимое сопротивление вторичного контура, обусловленное влиянием первичного контура.

Полагая, что контурные токи (13.1), (13.2) обусловлены действием э.д.с. 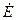и 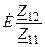определим эквивалентные сопротивления контуров, учитывающие их взаимное влияние,

;

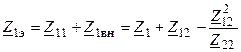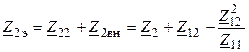
Поскольку в рассматриваемых цепях (рис. 13.1) используется реактивное сопротивление связи 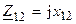, то при индуктивной связи между контурами это сопротивление положительно 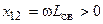, а при ёмкостной связи — отрицательно .

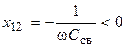Определим вносимое сопротивление первичного контура

,

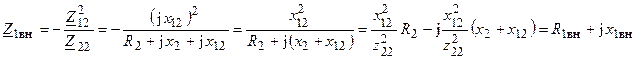где 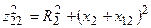— модуль комплексного сопротивления вторичного контура; 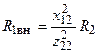, 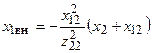— активная и реактивная составляющие вносимого сопротивления первичного контура.

Аналогично определяется вносимое сопротивление вторичного контура

,

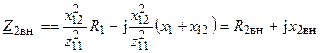где 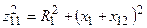— модуль комплексного сопротивления первичного контура; 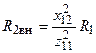, 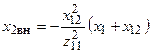— активная и реактивная составляющие вносимого сопротивления вторичного контура.

В результате, эквивалентные сопротивления контуров будут иметь вид

;

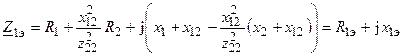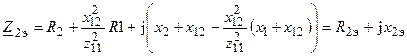
Из полученных выражений следует, что активные составляющие вносимых сопротивлений всегда положительны, а реактивные составляющие противоположны по знаку реактивным составляющим собственных комплексных сопротивлений контуров.

Если резонансные частоты контуров одинаковы и равны частоте источника напряжения, то в обоих контурах на этой частоте будет иметь место резонанс напряжений, при котором реактивные составляющие комплексных сопротивлений контуров равны нулю 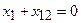и 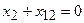. При этом реактивные составляющие вносимых сопротивлений будут также равны нулю 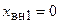, , 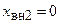а активные составляющие будут иметь максимальные значения 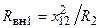, , 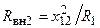поскольку при резонансе 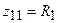и .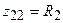

Лекция 16