Расстояние от точки до прямой
Пусть на плоскости относительно прямоугольной системы координат 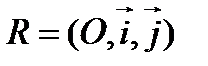 прямая
прямая 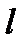 задается уравнением
задается уравнением 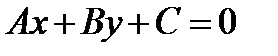 , где
, где 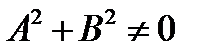 .
.
Расстояние от точки 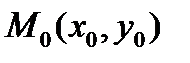 до прямой
до прямой 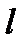 равняется длине перпендикуляра
равняется длине перпендикуляра 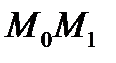 , проведенного из
, проведенного из 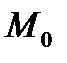 к прямой
к прямой 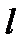 .
.
Так как 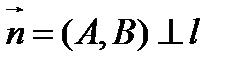 , то
, то 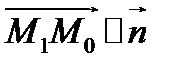 .
.
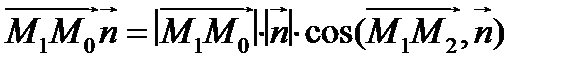 . Так как
. Так как 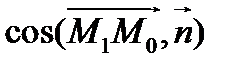 равен либо
равен либо 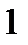 , либо
, либо 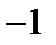 , то получаем
, то получаем
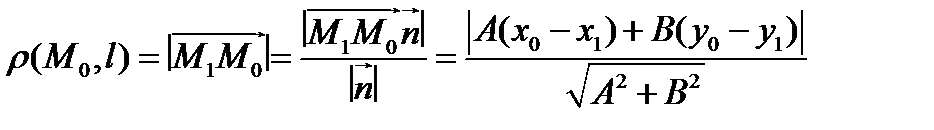 . Учитывая, что
. Учитывая, что 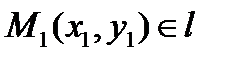 , то есть
, то есть 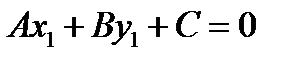 , получаем формулу для вычисления расстояния от точки до прямой
, получаем формулу для вычисления расстояния от точки до прямой
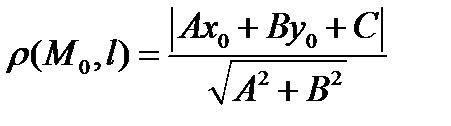 .
.
Взаимное расположение двух прямых на плоскости
Относительно аффинной системы координат 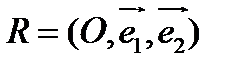 прямые
прямые 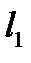 и
и 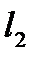 задаются уравнениями
задаются уравнениями
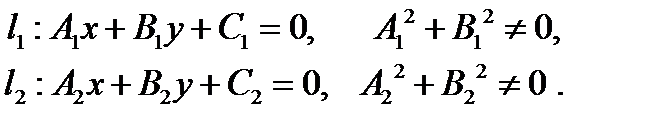
Для каждой прямой можно найти точку, принадлежащую этой прямой, и направляющий вектор
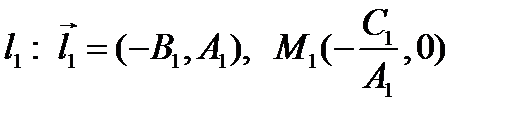 , если
, если 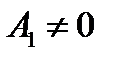 ;
;
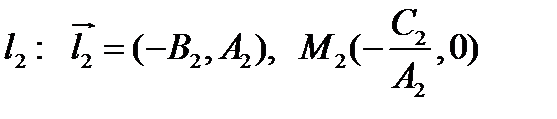 , если
, если 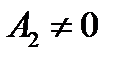
1. 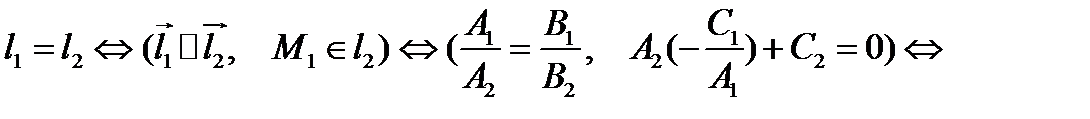
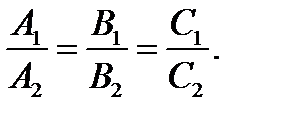
Прямые совпадают тогда и только тогда, когда в их общих уравнениях коэффициенты и свободные члены пропорциональны.
2. 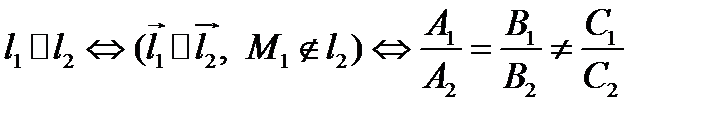 .
.
Прямые параллельны тогда и только тогда, когда в их общих уравнениях коэффициенты пропорциональны, но не пропорциональны свободным членам.
3. 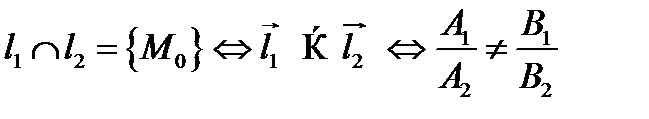
Прямые пересекаются в точке тогда и только тогда, когда в их общих уравнениях коэффициенты не пропорциональны.
Угол между прямыми
Углом между прямыми 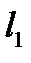 и
и 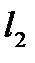 называется величина того из четырех вертикальных углов, образованных этими прямыми, который не превосходит остальные углы. Таким образом, угол
называется величина того из четырех вертикальных углов, образованных этими прямыми, который не превосходит остальные углы. Таким образом, угол 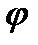 между прямыми может принимать значения от 0 до
между прямыми может принимать значения от 0 до 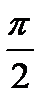 .
.
Иногда удобно угол между прямыми считать направленным. Угол между прямыми 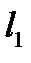 и
и 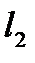 , заданными в указанном порядке, будем считать положительным, если поворот от
, заданными в указанном порядке, будем считать положительным, если поворот от 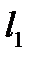 к
к 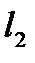 по этому углу совершается против часовой стрелки. В противном случае угол будем считать отрицательным.
по этому углу совершается против часовой стрелки. В противном случае угол будем считать отрицательным.
Пусть на плоскости относительно прямоугольной системы координат 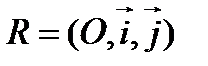 прямые
прямые 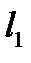 и
и 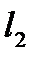 задаются уравнениями
задаются уравнениями
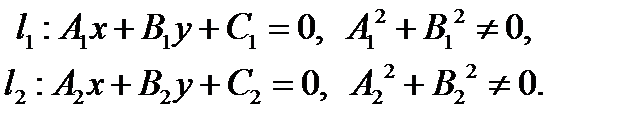
Тогда 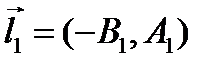 ,
, 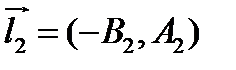 .
.
Угол 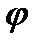 между прямыми
между прямыми 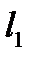 и
и 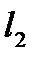 равен
равен 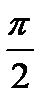 тогда и только тогда, когда направляющие векторы прямых ортогональны и, следовательно,
тогда и только тогда, когда направляющие векторы прямых ортогональны и, следовательно, 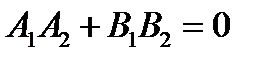 .
.
Если угол 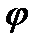 между прямыми отличен от
между прямыми отличен от 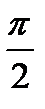 , то он однозначно определяется по значению его тангенса.
, то он однозначно определяется по значению его тангенса.
Заметим, что тангенс направленного угла между прямыми равен тангенсу направленного угла между направляющими векторами этих прямых: 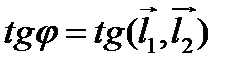 .
.
Как вычислить тангенс направленного угла 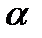 между векторами
между векторами 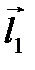 и
и 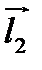 ?
?
Пусть 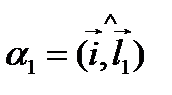 и
и 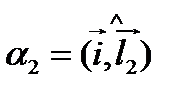 направленные углы между вектором
направленные углы между вектором 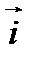 и направляющими векторами прямых. Для направленного угла
и направляющими векторами прямых. Для направленного угла 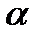 между векторами
между векторами 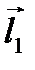 и
и 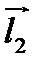 имеем
имеем 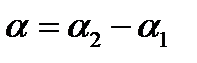 .
.
Для вычисления 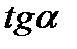 найдем
найдем 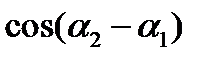 и
и 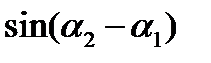 :
:
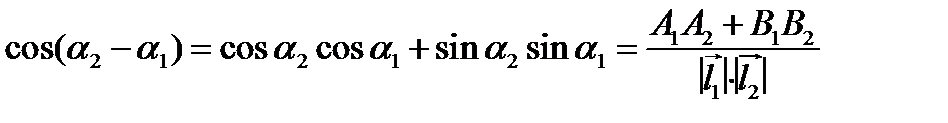 .
.
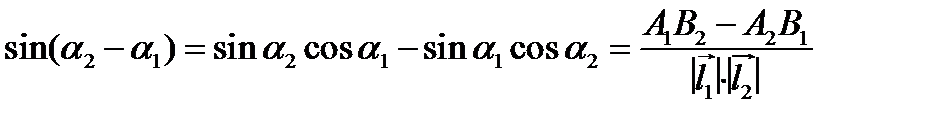 .
.
Таким образом, 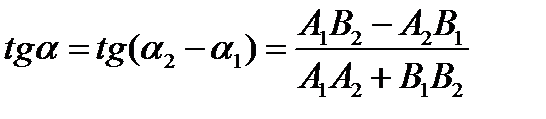 .
.
Возможны случаи
а) 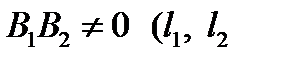 не параллельны оси
не параллельны оси 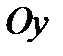 )
)
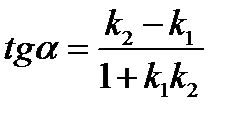 , где
, где 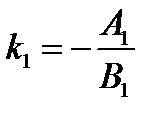 и
и 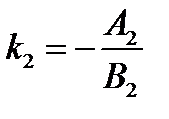 – угловые коэффициенты прямых
– угловые коэффициенты прямых 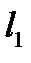 и
и 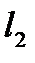 .
.
б) 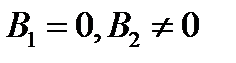 , (
, ( 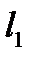 параллельна, а
параллельна, а 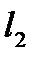 не параллельна оси
не параллельна оси 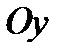 ).
).
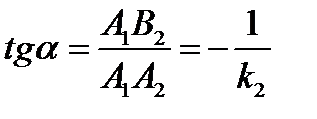 .
.
в) 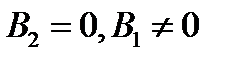 (
( 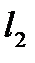 параллельна, а
параллельна, а 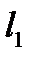 не параллельна оси
не параллельна оси 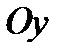 ).
).
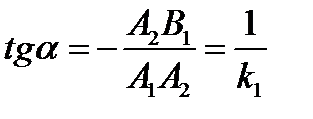 .
.
г) 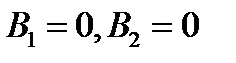 , (прямые параллельны оси
, (прямые параллельны оси 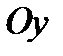 ).
).
Дата добавления: 2021-09-25; просмотров: 495;











