Геометрический смысл знака трехчлена прямой
Каждая прямая плоскости разделяет эту плоскость на две части, называемые полуплоскостями. Две точки одной и той же полуплоскости лежат по одну сторону от данной прямой. Любые две точки, принадлежащие различным полуплоскостям, лежат по разные стороны от прямой. Как аналитически, то есть по уравнению прямой и координатам точек определить, лежат эти точки в одной или в разных полуплоскостях относительно данной прямой?
Относительно аффинной системы координат 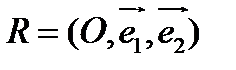 прямая задана уравнением
прямая задана уравнением 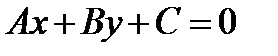 , где
, где 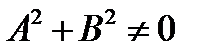 .
.
Обозначим 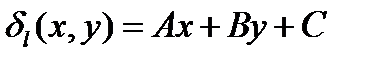 – трехчлен прямой.
– трехчлен прямой.
Для точек 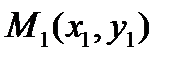 и
и 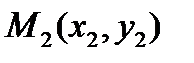 , не лежащих на прямой
, не лежащих на прямой 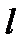 , будем иметь
, будем иметь 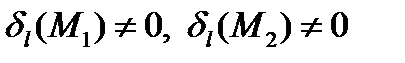 .
.
Точки 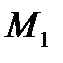 и
и 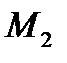 лежат по разные стороны от прямой
лежат по разные стороны от прямой 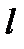 тогда и только тогда, когда отрезок
тогда и только тогда, когда отрезок 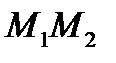 пересекает прямую
пересекает прямую 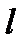 в некоторой точке
в некоторой точке 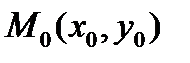 .
.
Так как точка 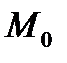 лежит между
лежит между 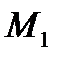 и
и 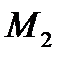 , то
, то 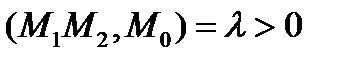 и
и 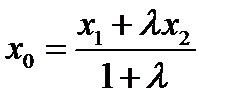 ,
, 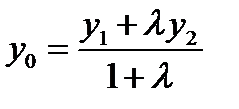 .
.
Точка 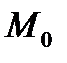 лежит на прямой
лежит на прямой 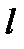 , поэтому
, поэтому 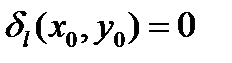 . Отсюда получаем
. Отсюда получаем 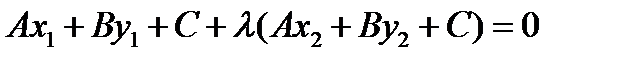 и
и 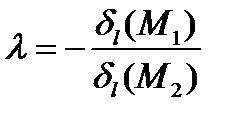 , а значит
, а значит 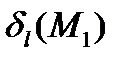 и
и 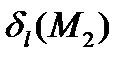 разных знаков.
разных знаков.
Таким образом, две точки 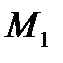 и
и 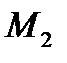 лежат по разные стороны от прямой
лежат по разные стороны от прямой 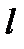 тогда и только тогда, когда значения трехчлена прямой для координат этих точек
тогда и только тогда, когда значения трехчлена прямой для координат этих точек 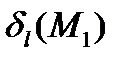 и
и 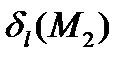 разных знаков.
разных знаков.
Имеем геометрический смысл знака трехчлена:
Каждое из неравенств 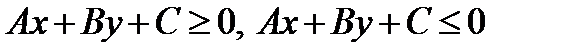 определяет полуплоскость с границей
определяет полуплоскость с границей 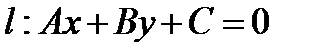 .
.
Дата добавления: 2021-09-25; просмотров: 571;











