Метод координат на плоскости

Задавая на плоскости аффинную систему координат, мы устанавливаем взаимно однозначное соответствие между точками и упорядоченными парами действительных чисел. Это позволяет находить условие, определяющее геометрическую фигуру.

Под условием, определяющим геометрическую фигуру, понимаем упорядоченные пары действительных чисел, уравнения, неравенства или их системы, которым удовлетворяют координаты любой точки, принадлежащей фигуре, и не удовлетворяют координаты точек, не принадлежащих фигуре.

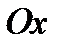Например, относительно аффинной системы координат прямая, совпадающая с осью , задается уравнением , полуплоскость с границей задается неравенством 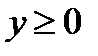, точки первой координатной четверти задаются системой неравенств .

Тогда геометрическую задачу можно перевести на язык алгебры, решить методами алгебры и полученный результат интерпретировать геометрически.

О п р е д е л е н и е. Линия на плоскости называется алгебраической, если существует аффинная система координат, в которой уравнение этой линии имеет вид , где 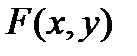– многочлен, то есть сумма членов вида ( – действительное число, 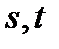- целые, неотрицательные числа).

Число 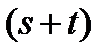называется степенью члена , где .

Степень многочлена 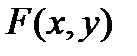– это наибольшая из степеней его членов.

Степень многочлена 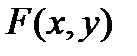называется порядком алгебраической линии.

Пример. Относительно прямоугольной системы координат окружность с центром 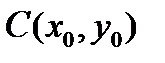радиуса задается уравнением . Следовательно, окружность является алгебраической линией второго порядка.

Используя формулы (1) из §2 преобразования координат точек при замене системы координат, можно найти уравнение алгебраической линии в новой системе координат. При этом несложно убедиться в справедливости следующей теоремы

Т е о р е м а. Понятие алгебраической линии и её порядок не зависят от выбора аффинной системы координат.

Кроме алгебраических, существует бесконечно много неалгебраических (трансцендентных) линий. К ним, в частности, относятся линии, задаваемые уравнениями: .