Директориальное свойство эллипса и гиперболы
О п р е д е л е н и е. Директрисой эллипса (гиперболы) называется прямая, перпендикулярная фокальной оси и отстоящая от второй оси на расстоянии 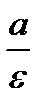 .
.
Таким образом, для эллипса и гиперболы, заданных каноническими уравнениями 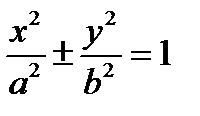 , директрисы задаются уравнениями
, директрисы задаются уравнениями 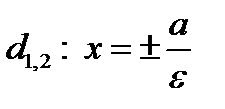 .
.
Имеет место следующая теорема
Т е о р е м а. Эллипс (гипербола) есть множество всех точек плоскости, отношение расстояний от которых до фокуса к расстоянию до соответствующей директрисы равно эксцентриситету.
Д о к а з а т е л ь с т в о.Фактически требуется доказать совпадение двух множеств: эллипса (гиперболы) и множества точек, обладающих указанным в теореме свойством. Таким образом, достаточно показать включение каждого из этих множеств в другое.
1. Для любой точки 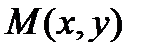 , принадлежащей эллипсу (гиперболе), её координаты удовлетворяют уравнению
, принадлежащей эллипсу (гиперболе), её координаты удовлетворяют уравнению 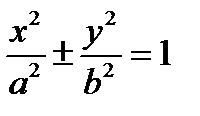 . Кроме того, для этих линий соответственно имеем соотношения:
. Кроме того, для этих линий соответственно имеем соотношения: 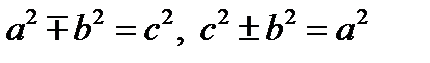 . Учитывая это, можно подсчитать
. Учитывая это, можно подсчитать 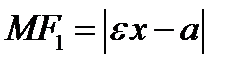 . Так как
. Так как 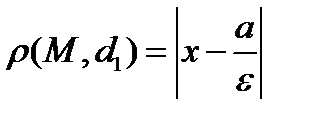 , то получаем
, то получаем 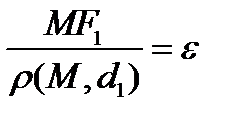 . Таким образом, имеет место включение всех точек эллипса (гиперболы) во множество точек, отношение расстояний от которых до фокуса к расстоянию до соответствующей директрисы равно эксцентриситету.
. Таким образом, имеет место включение всех точек эллипса (гиперболы) во множество точек, отношение расстояний от которых до фокуса к расстоянию до соответствующей директрисы равно эксцентриситету.
2. Пусть для точки 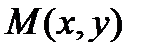 имеет место равенство
имеет место равенство 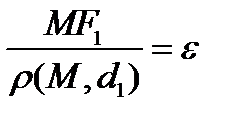 . Получаем
. Получаем 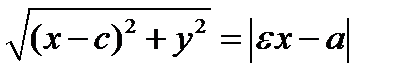 или
или
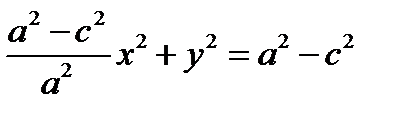 .(*)
.(*)
Если 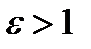 , то
, то  и
и 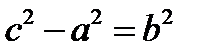 . Уравнение (*) определяет гиперболу
. Уравнение (*) определяет гиперболу 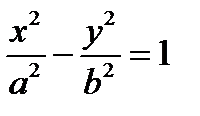 . То есть точка
. То есть точка 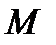 принадлежит гиперболе.
принадлежит гиперболе.
Если 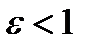 , то
, то  ,
, 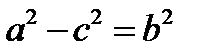 и уравнение (*) определяет эллипс
и уравнение (*) определяет эллипс 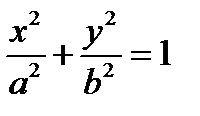 . То есть точка
. То есть точка 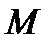 принадлежит эллипсу.
принадлежит эллипсу.
Таким образом, для множества точек, отношение расстояний от которых до фокуса к расстоянию до соответствующей директрисы равно эксцентриситету, показали его включение во множество точек эллипса (гиперболы).
Из пунктов 1, 2 следует справедливость утверждения теоремы.
Дата добавления: 2021-09-25; просмотров: 659;











