Приведение общего уравнения линии второго порядка к каноническому виду
Из определения алгебраической линии следует, что в произвольной аффинной системе координат 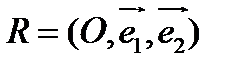 уравнение линии второго порядка имеет вид:
уравнение линии второго порядка имеет вид:
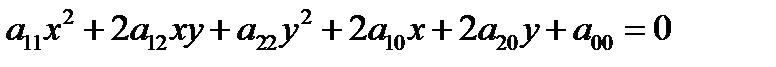 , (1)
, (1)
где 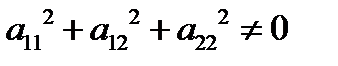 .
.
Уравнение (1) называется общим уравнением алгебраической линии второго порядка.
Пусть относительно прямоугольной системы координат 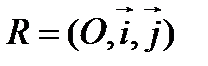 линия второго порядка задана уравнением (1).
линия второго порядка задана уравнением (1).
Т е о р е м а. Для каждой линии второго порядка, заданной в прямоугольной системе координат уравнением (1), существует прямоугольная система координат 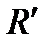 , в которой линия задаётся уравнением, не содержащим члена с произведением текущих координат, то есть уравнением вида
, в которой линия задаётся уравнением, не содержащим члена с произведением текущих координат, то есть уравнением вида
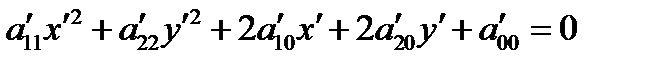 (2).
(2).
Д о к а з а т е л ь с т в о. Имеем формулы преобразования координат при повороте осей координат на угол 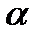
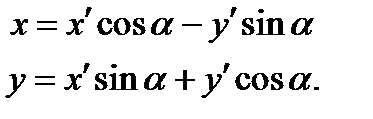 (3)
(3)
Чтобы найти уравнение линии в новой системе координат, нужно в уравнение (1) подставить выражения (3) старых координат через новые. Будем искать такой угол 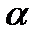 поворота осей координат, чтобы в новом уравнении коэффициент при
поворота осей координат, чтобы в новом уравнении коэффициент при 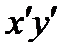 был равен нулю:
был равен нулю:
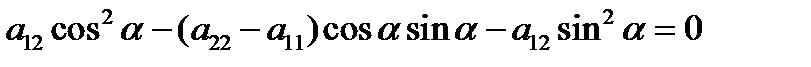 . (4)
. (4)
В уравнении (4) 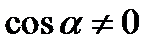 . В противном случае, получим
. В противном случае, получим 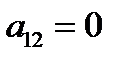 , то есть уравнение (1) уже имеет требуемый вид.
, то есть уравнение (1) уже имеет требуемый вид.
Из однородного уравнения (4) находим два значения угла 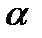 , для которых коэффициент при произведении текущих координат обращается в нуль. Можно выбрать любой из них. При повороте осей координат системы
, для которых коэффициент при произведении текущих координат обращается в нуль. Можно выбрать любой из них. При повороте осей координат системы 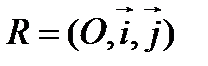 на этот угол получим искомый репер
на этот угол получим искомый репер 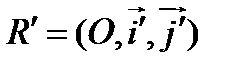 .
.
Пусть уравнение линии второго порядка приведено к виду (2). Возможны случаи
I. 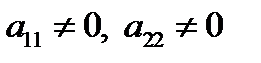 .
.
Выделив для 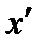 и
и 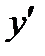 полные квадраты, получим уравнение вида
полные квадраты, получим уравнение вида
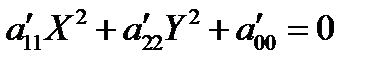 , (5)
, (5)
где обозначено 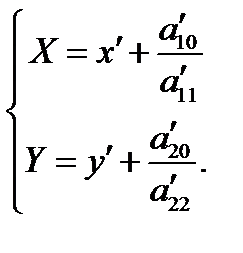
Отсюда получаем 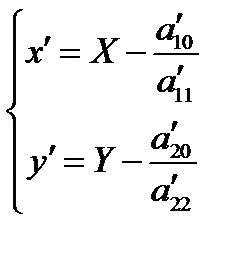 – формулы преобразования координат при переносе начала системы координат в точку
– формулы преобразования координат при переносе начала системы координат в точку 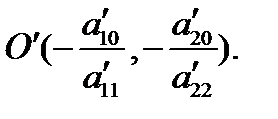
В зависимости от значений параметров 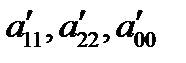 можно получить следующие канонические уравнения
можно получить следующие канонические уравнения
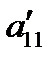
| 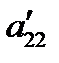
| 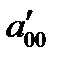
| Каноническое уравнение | Название линии |
| + | + | - | 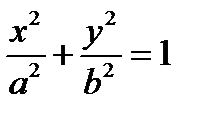
| Эллипс |
| - | - | + | ||
| + | + | + | 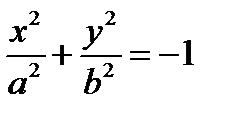
| Мнимый эллипс |
| - | - | - | ||
| + | - | 
| 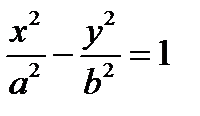
| Гипербола |
| - | + | |||
| + | + | 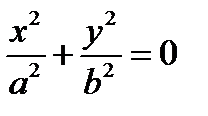
| Пара мнимых пересекающихся прямых | |
| - | - | |||
| + | - | 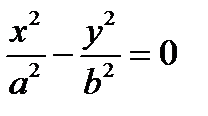
| Пара пересекающихся прямых | |
| - | + |
II. 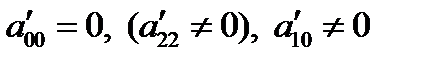 .
.
Уравнение (2) можно записать в виде
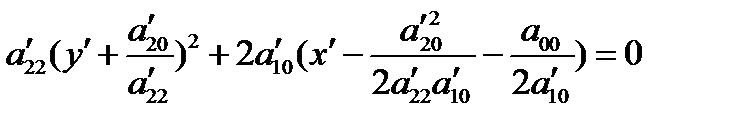 .
.
Обозначив 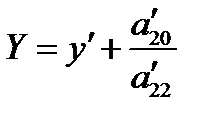 ,
, 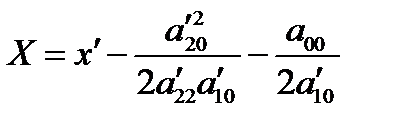 , получим каноническое уравнение параболы:
, получим каноническое уравнение параболы: 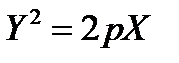 .
.
III. 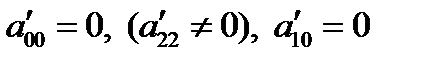 .
.
Уравнение линии приводится к виду 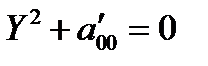 . В зависимости от значений параметра
. В зависимости от значений параметра 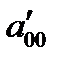 получаем
получаем
– 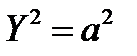 – каноническое уравнение пары параллельных прямых;
– каноническое уравнение пары параллельных прямых;
– 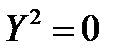 – каноническое уравнение пары совпавших прямых;
– каноническое уравнение пары совпавших прямых;
– 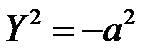 – каноническое уравнение пары мнимых параллельных прямых.
– каноническое уравнение пары мнимых параллельных прямых.
Таким образом, имеем 9 сортов линий второго порядка.
Чтобы привести уравнение линии второго порядка к каноническому виду, надо:
1. добиться, чтобы в группе старших членов исчез член с произведением текущих координат (поворот осей координат);
2. добиться, чтобы число членов первой степени стало наименьшим (выделение полных квадратов, перенос начала системы координат);
3. если возможно, уничтожить свободный член (перенос начала системы координат).
Дата добавления: 2021-09-25; просмотров: 588;











