Формулы преобразования координат
При изменении системы координат будут меняться координаты точек. Как будет происходить это изменение?
Перейдем от репера 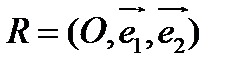 к реперу
к реперу 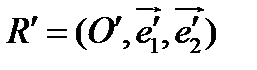 , где известны координаты точки
, где известны координаты точки 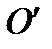 относительно репера
относительно репера 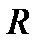 и координаты векторов
и координаты векторов 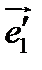 и
и 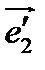 в базисе
в базисе 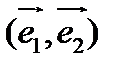 :
: 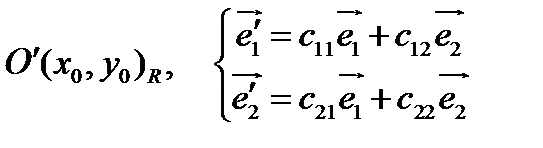 .
.
Здесь 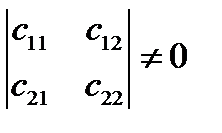 , так как векторы
, так как векторы 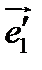 и
и 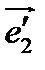 образуют базис.
образуют базис.
Для произвольной точки 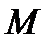 плоскости имеем координаты
плоскости имеем координаты 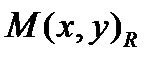 относительно репера
относительно репера 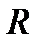 – старые координаты, и координаты
– старые координаты, и координаты 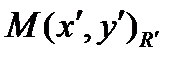 относительно репера
относительно репера  – новые координаты. Выразим старые координаты точки через её новые координаты. Имеем
– новые координаты. Выразим старые координаты точки через её новые координаты. Имеем
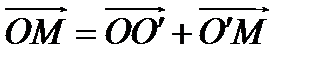 . (1)
. (1)
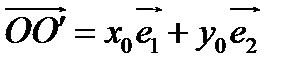 (
( 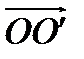 – радиус-вектор точки
– радиус-вектор точки 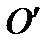 в репере
в репере 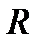 ).
).
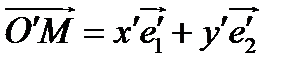 (
( 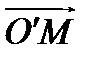 – радиус-вектор точки
– радиус-вектор точки 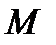 в репере
в репере 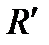 ).
).
Учитывая это и разложение векторов 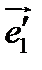 и
и 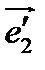 по векторам базиса
по векторам базиса 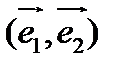 , из (1) получим формулы преобразования координат при замене аффинного репера:
, из (1) получим формулы преобразования координат при замене аффинного репера:
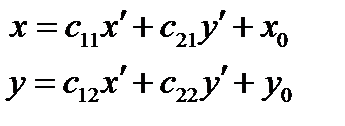 (*).
(*).
Если при замене репера 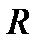 меняется только начало системы координат, то есть
меняется только начало системы координат, то есть 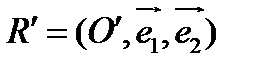 , то
, то 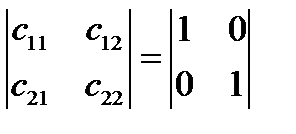 и формулы (*) принимают вид:
и формулы (*) принимают вид:
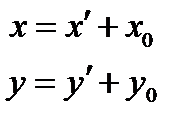 – формулы преобразования координат при переносе начала системы координат.
– формулы преобразования координат при переносе начала системы координат.
Произвольную замену репера можно осуществлять в два этапа: перенос начала системы координат и замена координатных векторов.
Особо рассмотрим преобразование прямоугольной системы координат.
Пусть реперы 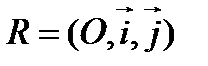 и
и 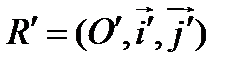 ориентированы одинаково. Отложив векторы
ориентированы одинаково. Отложив векторы 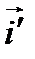 и
и 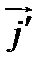 от точки
от точки  , найдем координаты этих векторов в базисе
, найдем координаты этих векторов в базисе 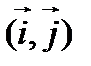 .
.
Имеем 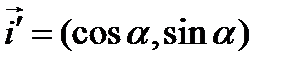 ,
, 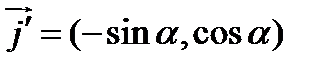 , где
, где 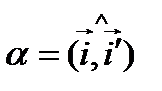 .
.
Формулы (*) примут вид
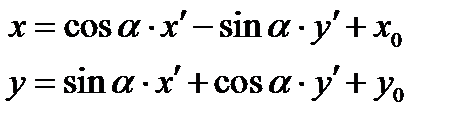 (**).
(**).
Из них, в частности, получим формулы преобразования координат при повороте осей прямоугольной системы координат на угол 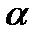 :
:
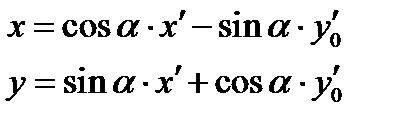
Проведя аналогичные рассуждения в случае противоположно ориентированных реперов 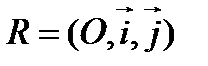 и
и 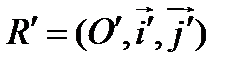 , получим формулы
, получим формулы
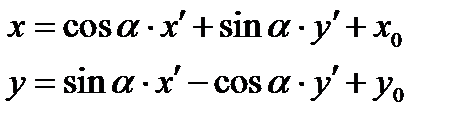 (***).
(***).
Формулы (**) и (***) можно записать в общем виде
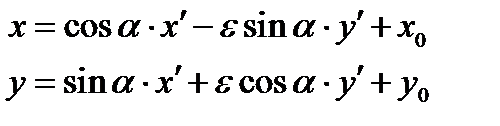 ,
,
где 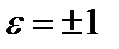 .
.
Дата добавления: 2021-09-25; просмотров: 656;











