Скорость поступательного движения образует с осью вращательного движения НМС произвольный угол

Сложное движение в этом случае состоит из переносного поступательного движения и относительного вращательного движения НМС и представляет собой общий случай движения НМС (глава 6).

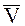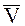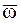Для нахождения абсолютного движения НМС разложим вектор в плоскости xОz, положение которой определяется векторами и , на составляющие, направленные по оси вращения и перпендикулярно к ней (рис. 87):

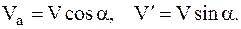
Используя случай 8.5.1 для 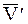и 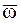, получим мгновенное вращательное движение вокруг мгновенной оси О₁z', параллельной оси Oz и отстоящей от нее на расстоянии 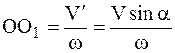. При этом угловая скорость 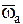НМС равна по модулю и направлению данной угловой скорости .

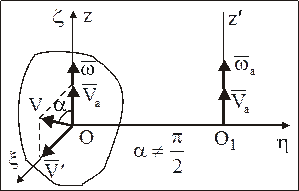
Рис. 87

Так как составляющая скорости поступательного движения НМС является свободным вектором, то ее можно перенести параллельно самой себе в точку О₁ и, таким образом, в точке О₁ получим случай, рассмотренный в п. 8.5.2, .

Если НМС участвует в поступательном движении со скоростью 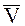и во вращательном движении с угловой скоростью 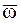, образующей произвольный угол 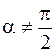со скоростью 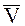, то абсолютное движение НМС будет мгновенным винтовым движением со скоростью поступательного движения 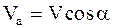и угловой скоростью 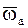, равной по модулю и направлению данной угловой скорости 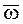, с мгновенной винтовой осью, параллельной оси данного вращения и отстоящей от нее на расстоянии, равном .

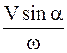Теорема: Совокупность движений НМС, определяемых мгновенной угловой скоростью 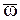и поступательной скоростью 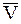, направленной не перпендикулярно к 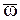, сводится к мгновенному винтовому движению около мгновенной винтовой оси.

Сложное движение НМС в этом случае совпадает с общим случаем движения НМС (глава 6) и может быть представлено в виде последовательных мгновенных винтовых движений относительно винтовых осей, положение которых будет непрерывно меняться.

Заключение