Вращение вокруг линии уровня
Задачу на определение натуральной величины плоской фигуры можно решить более быстрым способом, если за ось вращения выбрать линию уровня. Одним поворотом вокруг этой линии можно расположить данную плоскость параллельно одной из плоскостей проекций, вращая вокруг горизонтали - параллельно плоскости p1, вокруг фронтали - параллельно плоскости p2.
Рассмотрим пример на рис. 5.9.
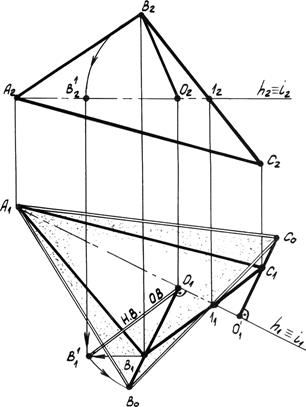
Рис. 5.9. Вращение вокруг горизонтали.
Горизонталь h плоскости (АВС) является осью вращения i. Точки А и 1 плоскости остаются неподвижными, т.к. расположены на оси вращения. Задача сводится к определению натуральной величины радиусов вращения двух точек плоскости В и С. Определяем радиусы вращения этих точек О1В1 ^ h1, 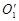 C1 ^ h1. Найдём натуральную величину радиуса ОВ вращением вокруг оси перпендикулярной плоскости p2 в точке О. О1В
C1 ^ h1. Найдём натуральную величину радиуса ОВ вращением вокруг оси перпендикулярной плоскости p2 в точке О. О1В 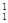 - натуральная величина ОВ, откладываем её на горизонтальной проекции радиуса, определяем положение точки В после вращения Вo. Через Вo и неподвижную точку 11 проводим прямую до пересечения с прямой
- натуральная величина ОВ, откладываем её на горизонтальной проекции радиуса, определяем положение точки В после вращения Вo. Через Вo и неподвижную точку 11 проводим прямую до пересечения с прямой 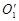 С1, по которой пересекается точка С. Определяем положение точки С после вращения - Сo. А1ВoСo – натуральная величина треугольника АВС, преобразованного в горизонтальную плоскость уровня. Фронтальная проекция плоскости треугольника после вращения преобразуется в прямую совпадающую с горизонталью плоскости h.
С1, по которой пересекается точка С. Определяем положение точки С после вращения - Сo. А1ВoСo – натуральная величина треугольника АВС, преобразованного в горизонтальную плоскость уровня. Фронтальная проекция плоскости треугольника после вращения преобразуется в прямую совпадающую с горизонталью плоскости h.
Дата добавления: 2016-11-26; просмотров: 7807;











