Односторонние пределы функции
Если отыскивается предел функции  при условии, что
при условии, что  , стремясь к
, стремясь к  , может принимать только такие значения, которые меньше
, может принимать только такие значения, которые меньше  , то этот предел, если он существует, называется левосторонним пределом функции
, то этот предел, если он существует, называется левосторонним пределом функции  . Для того, чтобы показать, что
. Для того, чтобы показать, что  стремится к
стремится к  , оставаясь меньше
, оставаясь меньше  , применяется запись
, применяется запись 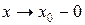
 .
.
Если отыскивается предел функции  при условии, что
при условии, что  , стремясь к
, стремясь к  , может принимать только такие значения, которые больше
, может принимать только такие значения, которые больше  , то этот предел, если он существует, называется правосторонним пределом функции. Для того, чтобы показать, что
, то этот предел, если он существует, называется правосторонним пределом функции. Для того, чтобы показать, что  стремится к
стремится к  , оставаясь больше
, оставаясь больше  , применяется запись
, применяется запись 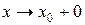
 .
.
Очевидно, что предел функции  при
при 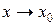 существует тогда и только тогда, когда существуют и равны между собой ее левосторонний и правосторонний пределы
существует тогда и только тогда, когда существуют и равны между собой ее левосторонний и правосторонний пределы 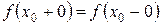 . В связи с этим можно дать еще одно определение непрерывной функции.
. В связи с этим можно дать еще одно определение непрерывной функции.
Определение 3. Функция  называется непрерывной при
называется непрерывной при 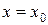 , если ее правосторонний и левосторонний пределы существуют, равны между собой и равны значению функции в этой точке
, если ее правосторонний и левосторонний пределы существуют, равны между собой и равны значению функции в этой точке
 .
.
Пример.
Рассмотренная в разделе 4 функция  не имеет предела в точке
не имеет предела в точке 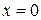 . Однако, если ограничиться рассмотрением только положительных
. Однако, если ограничиться рассмотрением только положительных  , то предел при
, то предел при  , стремящемся к 0, существует и равен +1
, стремящемся к 0, существует и равен +1
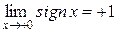 .
.
Если же рассматривать только отрицательные  , то предел при
, то предел при  , стремящемся к 0, существует и равен –1
, стремящемся к 0, существует и равен –1
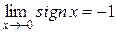 .
.
Дата добавления: 2021-09-25; просмотров: 558;











