Свойства непрерывных функций
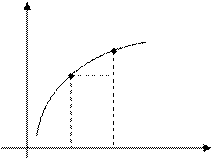 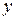
| Пусть функция 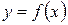 определена при некотором значении определена при некотором значении  , т.е. , т.е. 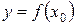 , и в некоторой окрестности , и в некоторой окрестности  . .
| ||||||||||
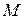
| |||||||||||
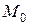
| 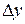
| ||||||||||
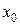 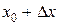 
|
Определение 1. Функция 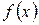 называется непрерывной в точке
называется непрерывной в точке 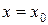 , если в этой точке бесконечно малому приращению аргумента соответствует бесконечно малое приращение функции, т.е.
, если в этой точке бесконечно малому приращению аргумента соответствует бесконечно малое приращение функции, т.е. 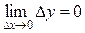 .
.
Определение 2. Если предел функции 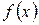 при
при 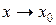 существует и равен значению функции в точке
существует и равен значению функции в точке 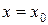 , то функция
, то функция 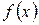 называется непрерывной при
называется непрерывной при 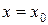 , т.е. для непрерывной функции должно выполняться равенство
, т.е. для непрерывной функции должно выполняться равенство
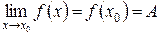 .
.
Причем для непрерывности функции при 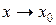 это равенство должно выполняться при стремлении
это равенство должно выполняться при стремлении  к
к  по любому закону.
по любому закону.
Для того, чтобы функция 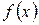 была непрерывной при
была непрерывной при 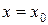 , требуется выполнение трех условий:
, требуется выполнение трех условий:
1. Точка  должна принадлежать области определения функции. Функция
должна принадлежать области определения функции. Функция 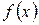 должна быть определена не только в самой точке
должна быть определена не только в самой точке  , но и в некоторой ее окрестности.
, но и в некоторой ее окрестности.
2. Функция 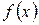 должна иметь конечный предел при
должна иметь конечный предел при 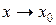 :
: 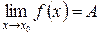 .
.
3. Предел 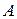 должен быть равен значению функции в точке
должен быть равен значению функции в точке 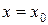 ,
, 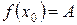 .
.
Если соотношение 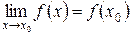 не имеет место для функции
не имеет место для функции 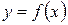 в данной точке
в данной точке 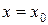 , то функция называется разрывной в точке
, то функция называется разрывной в точке 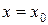 , а сама точка называется точкой разрыва.
, а сама точка называется точкой разрыва.
Функция непрерывная в каждой точке некоторой области (интервала, отрезка) называется непрерывной в этой области.
Пример. Доказать, что функция 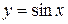 непрерывна в произвольной точке
непрерывна в произвольной точке  .
.
Доказательство. Пусть функция 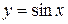 определена в точке
определена в точке  и
и 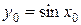 , тогда в точке
, тогда в точке 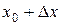
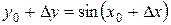 и приращение функции
и приращение функции 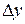 , когда приращение аргумента
, когда приращение аргумента 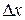 , имеет вид
, имеет вид
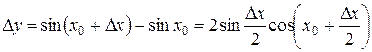 .
.
Найдем предел 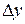 при
при 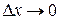
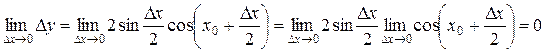 .
.
Следовательно, функция 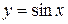 непрерывна в произвольной точке
непрерывна в произвольной точке  .
.
Аналогичным образом рассматривая каждую основную элементарную функцию, можно доказать теорему:
Всякая элементарная функция непрерывна в каждой точке, в которой она определена.
Непрерывная на отрезке 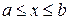 функция достигает на этом отрезке по меньшей мере один раз наибольшего значения
функция достигает на этом отрезке по меньшей мере один раз наибольшего значения 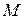 и наименьшего значения
и наименьшего значения 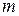 .
.
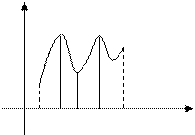 
| Необходимо иметь в виду, что утверждение теоремы о существовании наибольшего значения функции может оказаться неверным, если рассматривать значение функции на интервале 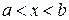 . .
| ||||||||
| 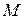
| ||||||||
| |||||||||
1. Пусть функция 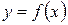 непрерывна на отрезке
непрерывна на отрезке 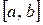 и на концах этого отрезка принимает значение разных знаков, тогда между точками
и на концах этого отрезка принимает значение разных знаков, тогда между точками 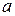 и
и 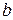 найдется по крайней мере одна точка
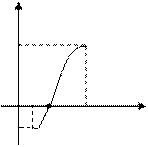
найдется по крайней мере одна точка 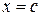 , в которой функция
, в которой функция  обратится в 0.
обратится в 0.
| 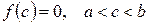 . .
| ||||||
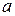 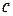
| |||||||
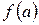
| 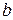
| 
| |||||
2. Пусть функция 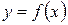 определена и непрерывна на отрезке
определена и непрерывна на отрезке 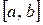 . Если на концах этого отрезка функция принимает неравные значения
. Если на концах этого отрезка функция принимает неравные значения 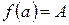 ,
, 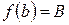 , то каково бы ни было число
, то каково бы ни было число 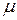 , заключенное между числами
, заключенное между числами 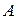 и
и 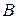 ,
, 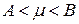 , найдется такая точка
, найдется такая точка 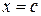 , заключенная между
, заключенная между 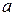 и
и 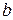 ,
, 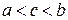 , что
, что 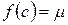 .
.
3. Сумма, разность, произведение и частное двух функций, непрерывных в одной и той же точке  , есть функция непрерывная в той же точке (в случае частного предполагается, что функция делитель не обращается в 0 при
, есть функция непрерывная в той же точке (в случае частного предполагается, что функция делитель не обращается в 0 при 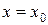 ).
).
Дата добавления: 2021-09-25; просмотров: 549;











