Второй замечательный предел
Функция 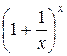 стремится при
стремится при  , стремящемся к бесконечности, к пределу
, стремящемся к бесконечности, к пределу 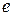 :
: 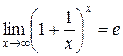 ,
,
где, 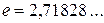 - основание натуральных логарифмов. Этот предел называется вторым замечательным пределом и используется всегда при нахождении пределов вида “
- основание натуральных логарифмов. Этот предел называется вторым замечательным пределом и используется всегда при нахождении пределов вида “ 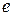 ”. Здесь основание системы
”. Здесь основание системы 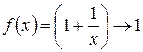 , когда
, когда 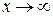 . Таким образом, имеем дело со случаем неопределенности вида
. Таким образом, имеем дело со случаем неопределенности вида 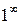 .
.
Если в этом пределе положить 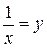 , то при
, то при 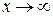 имеем
имеем 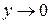 (но
(но 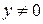 ) и получаем:
) и получаем: 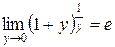 .
.
При отыскании пределов, связанных с неопределенностью вида 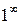 , надо так преобразовать исходную функцию, чтобы появились вышеупомянутые выражения. Чаще всего используется следующий общий прием.
, надо так преобразовать исходную функцию, чтобы появились вышеупомянутые выражения. Чаще всего используется следующий общий прием.
Пусть 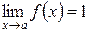 , а
, а 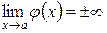 , тогда предел
, тогда предел 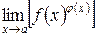 находим так. Представим функцию
находим так. Представим функцию 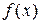 в виде
в виде 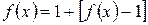 . Показатель степени
. Показатель степени 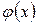 записываем в виде:
записываем в виде:
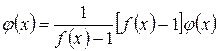
тогда
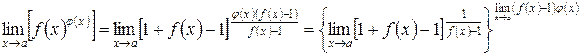 .
.
Делаем подстановку 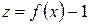 . Так как при
. Так как при 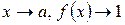 , то
, то 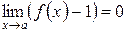 , т.е.
, т.е. 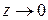 при
при 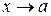 . Поэтому справедливо соотношение
. Поэтому справедливо соотношение
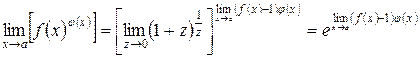 .
.
Нахождение предела функции сводится к нахождению предела 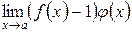 . (Подчеркнем, что
. (Подчеркнем, что 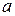 может быть и числом и одним из символов
может быть и числом и одним из символов 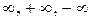 ).
).
Пример. Найти 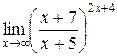 .
.
Решение. Основание степени 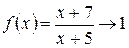 , когда
, когда 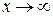 , а показатель степени
, а показатель степени 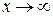 . Находим
. Находим 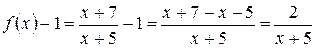 . Показатель степени представляем в виде
. Показатель степени представляем в виде
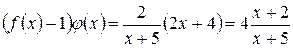
и находим его предел
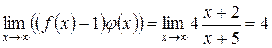 .
.
В результате получим
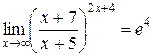 .
.
В ряде случаев использование общего приема приводит к ненужным усложнениям и пример можно решить гораздо проще.
Пример. Найти 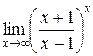 .
.
Решение. Основание степени 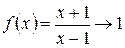 , когда ,
, когда , 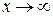 . Таким образом, имеет место случай неопределенности вида
. Таким образом, имеет место случай неопределенности вида 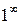 . Разделим числитель и знаменатель дроби на
. Разделим числитель и знаменатель дроби на  , и получим
, и получим
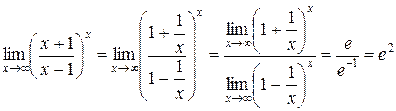 .
.
Пример. Найти 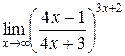 .
.
Решение. Основание степени 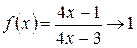 , когда
, когда 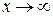 , а показатель степени стремится к бесконечности, поэтому приведем рассматриваемую дробь к виду, позволяющему использовать второй замечательный предел. Можно записать
, а показатель степени стремится к бесконечности, поэтому приведем рассматриваемую дробь к виду, позволяющему использовать второй замечательный предел. Можно записать
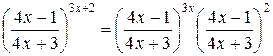 .
.
Учитывая, что предел второго сомножителя 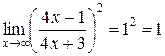 и разделив числитель и знаменатель дроби на
и разделив числитель и знаменатель дроби на 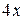 , перейдем к пределу в числителе и знаменателе дроби
, перейдем к пределу в числителе и знаменателе дроби
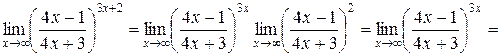
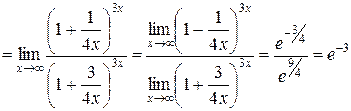 .
.
| Очень часто второй замечательный предел используется для нахождения пределов выражений, содержащих логарифмические и показательные функции. Тут следует учесть, что под знаком логарифма можно переходить к пределу, однако надо следить, чтобы предел функции, стоящей под знаком логарифма был положительным числом, поскольку логарифмическая функция определена только для положительных значений аргумента. |
Пример. Найти 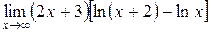 .
.
Решение. Учитывая свойства логарифмов, перепишем выражение, стоящее под знаком предела, в виде
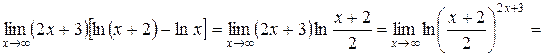
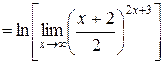 .
.
Выполненные преобразования корректны, поскольку функция, стоящая под знаком логарифма, при 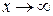 положительна. Поскольку
положительна. Поскольку
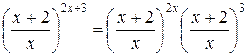
и предел второго сомножителя равен 1 при 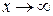
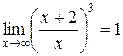 ,
,
то разделив числитель и знаменатель дроби на  , получим
, получим
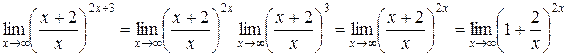
неопределенность вида 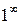 , при раскрытии которой можно воспользоваться вторым замечательным пределом
, при раскрытии которой можно воспользоваться вторым замечательным пределом
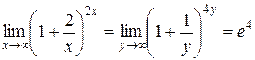 .
.
В результате получим
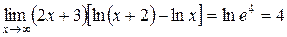 .
.
Пример. Найти 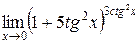 .
.
Решение. При 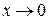
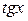 стремится к 0
стремится к 0 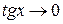 , а
, а 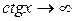 , поэтому имеем дело с неопределенностью вида
, поэтому имеем дело с неопределенностью вида 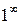 . Для того чтобы свести нахождение предела ко второму замечательному пределу, сделаем замену переменной, положив
. Для того чтобы свести нахождение предела ко второму замечательному пределу, сделаем замену переменной, положив 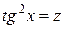 . Теперь следует и
. Теперь следует и 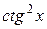 , стоящий в показатели степени, выразить через новую переменную
, стоящий в показатели степени, выразить через новую переменную 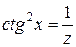 . Из равенства
. Из равенства 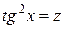 следует, что
следует, что 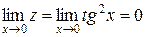 , поэтому новая переменная
, поэтому новая переменная 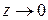 , когда
, когда 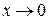 .
.
Получаем
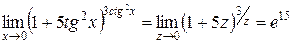 .
.
Очень часто при вычислении пределов встречаться с бесконечными функциями различного порядка малости.
Пусть 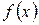 и
и 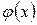 - бесконечно малые функции при
- бесконечно малые функции при 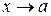 , т.е.
, т.е. 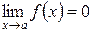 ,
, 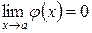 , тогда справедливы следующие определения:
, тогда справедливы следующие определения:
1. Если 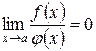 , то функция
, то функция 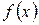 называется бесконечно малой функцией высшего порядка малости по сравнению с функцией
называется бесконечно малой функцией высшего порядка малости по сравнению с функцией 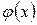 , а функция
, а функция 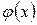 - низшего порядка малости по сравнению с функцией
- низшего порядка малости по сравнению с функцией 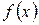 .
.
2. Если 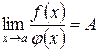 , (
, ( 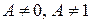 ), то бесконечно малые функции
), то бесконечно малые функции 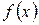 и
и 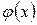 называются бесконечно малыми функциями одного порядка малости.
называются бесконечно малыми функциями одного порядка малости.
При вычислении предела алгебраической суммы (или разности) бесконечно малых функций можно пренебречь бесконечно малой функцией высшего порядка малости по сравнению с бесконечно малой функцией низшего порядка малости.
Пример. Найти 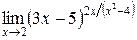 .
.
Решение. Основание степени 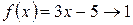 при
при 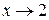 , а показатель
, а показатель 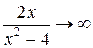 . Таким образом, имеет место неопределенность вида
. Таким образом, имеет место неопределенность вида 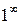 . Находим
. Находим 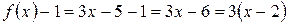 . Сделаем замену переменной, положив
. Сделаем замену переменной, положив 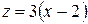 . При
. При 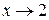
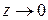 . Подставим в показатель степени
. Подставим в показатель степени  , выраженную через новую переменную
, выраженную через новую переменную 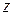 :
: 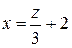
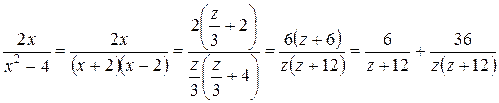 .
.
Получим
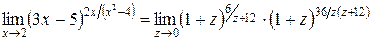 .
.
Предел первого сомножителя равен 1 при 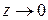 . Учитывая, что
. Учитывая, что 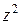 является бесконечно малой функцией высшего порядка по сравнению с бесконечно малой функцией
является бесконечно малой функцией высшего порядка по сравнению с бесконечно малой функцией 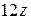
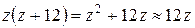 при
при 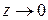
имеем
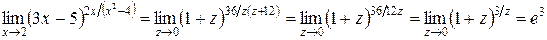 .
.
Этот пример можно решить гораздо проще, применяя общее правило.
Показатель степени представляем в виде
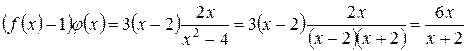
и находим его предел
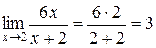 .
.
В результате получаем
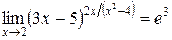 .
.
| Следует запомнить следующие пределы, которыми часто приходится пользоваться при решении примеров и которые являются следствием второго замечательного предела: |
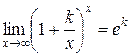 , ,
| 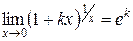 , ,
|
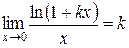 , ,
| 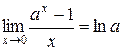 . .
|
КОНТРОЛЬНЫЕ ВОПРОСЫ
1. Сформулируйте первый замечательный предел.
2. Сформулируйте второй замечательный предел.
3. Что такое эквивалентные функции?
Дата добавления: 2021-09-25; просмотров: 589;











