Эквивалентные функции
Нахождение пределов тригонометрических выражений значительно упрощается, если использовать понятие об эквивалентных функциях.
Пусть 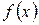 и
и 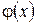 - бесконечно малые функции при
- бесконечно малые функции при  стремящемся к
стремящемся к 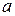 , т.е.
, т.е. 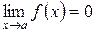 ,
, 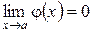 (причем
(причем 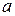 может быть как числом, так и
может быть как числом, так и 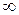 ,
, 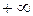 ,
, 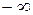 ). Если
). Если
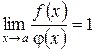 ,
,
то бесконечно малые функции 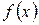 и
и 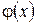 называются эквивалентными или равносильными. В этом случае пишут
называются эквивалентными или равносильными. В этом случае пишут 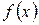 ~
~ 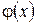 .
.
Теорема о замене бесконечно малых функций им эквивалентными гласит, что предел отношения двух бесконечно малых функций не изменится, если каждую из них или какую-либо одну заменить эквивалентными им.
Пример.Доказать, что при 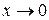 функции
функции 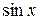 и
и 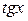 - эквивалентные бесконечно малые.
- эквивалентные бесконечно малые.
Если докажем, что 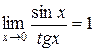 , то тем самым докажем, что
, то тем самым докажем, что 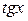 ~
~ 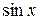 при
при 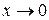 . Действительно,
. Действительно,
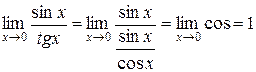 .
.
Полезно запомнить, что при 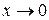 следующие функции являются эквивалентными
следующие функции являются эквивалентными
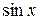 ~
~  ,
, 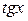 ~
~  ,
, 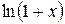 ~
~  ,
, 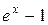 ~
~  ,
,
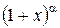 ~
~ 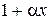 ,
, 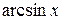 ~
~  ,
, 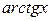 ~
~ 
и использовать эти соотношения при нахождении пределов. Эти соотношения эквивалентности остаются в силе и при 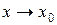 , если заменить в них
, если заменить в них  на функцию
на функцию 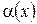 такую, что
такую, что 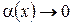 при
при 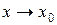 .
.
Пример. Найти 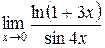 .
.
Решение. При 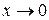 числитель и знаменатель дроби – функции бесконечно малые, более того,
числитель и знаменатель дроби – функции бесконечно малые, более того, 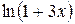 ~
~ 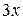 ,
, 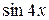 ~
~ 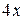 . Используя теорему о замене бесконечно малых функций им эквивалентными, получим
. Используя теорему о замене бесконечно малых функций им эквивалентными, получим
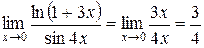 .
.
Пример. Найти 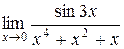 .
.
Решение. Так как при 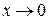 бесконечно малая функция
бесконечно малая функция 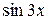 эквивалентна
эквивалентна 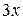 ,
, 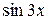 ~
~ 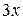 , то
, то
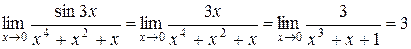 .
.
Дата добавления: 2021-09-25; просмотров: 584;











