Первый замечательный предел
Функция 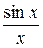 стремится при
стремится при  , стремящемся к нулю, к пределу, равному единице, т.е.
, стремящемся к нулю, к пределу, равному единице, т.е.
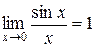 .
.
Этот предел называется первым замечательным пределом. Он представляет собой неопределённость вида 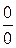 и используется, как правило, при нахождении пределов тригонометрических выражений. При этом неважно, какой вид имеет переменная
и используется, как правило, при нахождении пределов тригонометрических выражений. При этом неважно, какой вид имеет переменная  , главное, чтобы в числителе и знаменателе она была одной и той же.
, главное, чтобы в числителе и знаменателе она была одной и той же.
Пример. Найти 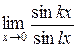 .
.
Решение. Числитель и знаменатель дроби при 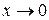 стремятся к нулю, поэтому приведём искомую дробь к виду, позволяющему использовать первый замечательный предел. Разделим числитель и знаменатель дроби на
стремятся к нулю, поэтому приведём искомую дробь к виду, позволяющему использовать первый замечательный предел. Разделим числитель и знаменатель дроби на  . Это можно сделать, так как значение
. Это можно сделать, так как значение  не должно рассматриваться
не должно рассматриваться
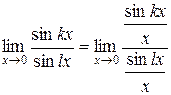 .
.
Сделаем в числителе подстановку 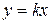 (отсюда следует, что
(отсюда следует, что 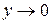 , когда
, когда 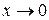 , а
, а 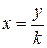 ), а в знаменателе подстановку
), а в знаменателе подстановку 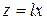 (отсюда следует, что
(отсюда следует, что 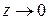 , когда
, когда 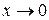 , а
, а 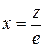 ). В результате получим
). В результате получим
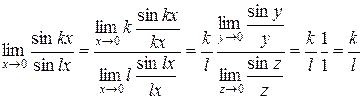 .
.
Необходимо подчеркнуть, что если под знаком предела стоит сумма или разность тригонометрических функций, а неопределённость имеет вид 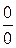 , то нужно так преобразовать их по известным формулам, чтобы получилось выражение вида
, то нужно так преобразовать их по известным формулам, чтобы получилось выражение вида 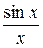 .
.
Пример. Найти 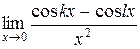 .
.
Решение. Числитель и знаменатель дроби при 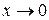 стремятся к нулю. Преобразуем числитель дроби
стремятся к нулю. Преобразуем числитель дроби
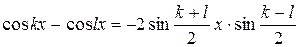
и применим приём, использованный в предыдущем примере

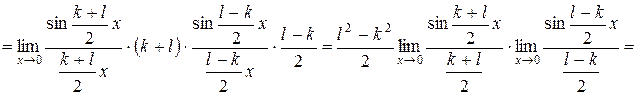
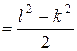 .
.
Пример. Найти  .
.
Решение. При 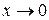 функция
функция 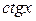 - бесконечно большая, а
- бесконечно большая, а  - величина бесконечно малая, т.е. мы имеем произведение функции бесконечно большой на бесконечно малую величину – неопределённость вида
- величина бесконечно малая, т.е. мы имеем произведение функции бесконечно большой на бесконечно малую величину – неопределённость вида 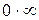 . Учтём, что
. Учтём, что  , тогда
, тогда
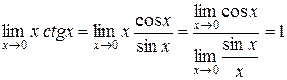 .
.
Дата добавления: 2021-09-25; просмотров: 515;











