Состояние системы. Уравнение состояния.

Системой тел или просто системой называется совокупность рассматриваемых тел. Примером системы может служить жидкость и находящийся в равновесии с ней пар.

Всякая система может находиться в различных состояниях, отличающихся температурой, давлением, объемом, плотностью, упругостью, степенью нагретости, степенью наэлектризованности, процентным соотношение между количествами разных веществ, из которых слагается тело, и т. д. Подобные величины, характеризующие состояние системы, называются параметрами состояний.

Не всегда какой-либо параметр имеет определенное значение. Если, например, температура в разных точках тела неодинакова, то телу нельзя приписать определенное значение параметра Т. В этом случае состояние называется неравновесным. Если такое тело изолировать от других тел и предоставить самому себе, то температура выравняется и примет одинаковое для всех точек значение Т – тело перейдет в равновесное состояние. Это значение Т не изменяется до тех пор, пока тело не будет выведено из равновесного состояния воздействием извне.

Итак, равновесным состоянием системы называется такое состояние, при котором все параметры системы имеют определенные значения, остающиеся при неизменных внешних условиях постоянными сколь угодно долго.

Важнейшими параметрами состояния систем являются: объем, давление и температура; они связаны между собой уравнением состояния:

f (p, v, T) = 0.

Вид функциональной зависимости между этими параметрами отыскивается для каждого данного вещества опытным путем. Только для разреженных газов, где молекулы движутся прямолинейно, точное уравнение состояния удается вывести теоретически.

Такие газы можно описать следующей моделью. Газ – это совокупность одинаковых, хаотически движущихся, не взаимодействующих друг с другом на расстоянии молекул. Размеры молекул столь малы, что суммарным объемом их можно пренебречь по сравнению с объемом сосуда. Подавляющую часть времени каждая молекула движется свободно, претерпевая иногда упругие соударения с другими молекулами или со стенками сосуда. Такая модель называется идеальным газом.

Для идеального газа количественная связь его параметров (макрохарактеристик) с характеристиками молекул (микрохарактеристиками) выражается основным уравнением молекулярно-кинетической теории:

,

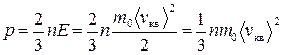где m₀ – масса отдельной молекулы, n – концентрация молекул, 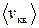– средняя квадратичная скорость, E – средняя кинетическая энергия поступательного движения молекулы. Согласно этому уравнению давление равно двум третям кинетической энергии поступательного движения молекул, заключенных в единице объема.

Учитывая, что температура есть проявление хаотического движения молекул и определяется их средней кинетической энергией поступательного движения

,

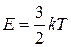где 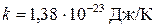– постоянная Больцмана, получим

.

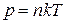Обозначая через N общее число молекул в объеме V газа и принимая во внимание, что 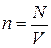, последнее уравнение представим в виде

.

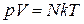Т. к. в n молях общее число молекул равно 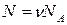, последнее уравнение может быть представлено в виде

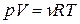
или

,

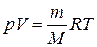где R = kN_A = 8,31441 Дж/(моль×К) – универсальная газовая постоянная. Данное уравнение называется уравнением Менделеева-Клапейрона (уравнением состояния идеального газа).

Газовые законы.

Из уравнения Менделеева-Клапейрона можно вывести ряд законов, справедливых для идеальных газов и полученных экспериментально.

Закон Бойля – Мариотта: произведение численных значений давления р и объема V идеального газа постоянно, если температура Т и масса газа m не изменяются, т. е. при Т = const и m = const

pV = const.

Закон Бойля – Мариотта характеризует связь между давлением и объемом идеального газа в изотермическом процессе изменения его состояния.

Закон Гей–Люссака: при постоянном давлении объем V данной массы m идеального газа прямо пропорционален его абсолютной температуре Т, т. е. при р = const и m = const

.

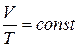Закон Гей–Люссака характеризует связь между объемом и температурой идеального газа в изобарическом процессе изменения его состояния.

Закон Шарля: при постоянных объеме V и массе m идеального газа давление газа р прямо пропорционально его абсолютной температуре Т, т. е. при V = const и m = const

.

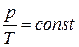Закон Шарля характеризует связь между давлением и температурой идеального газа в изохорическом процессе изменения его состояния.

8.5. Скорости теплового движения газовых молекул.

Все молекулы газа движутся с разными скоростями. Встречаются медленные молекулы, скорости которых близки к нулю. Встречаются очень быстрые молекулы, скорости которых во много раз превосходят средние скорости молекулярного движения. Между этими пределами скорости молекул с различной степенью вероятности принимают всевозможные значения. Закон распределения скоростей газовых молекул носит название распределения Максвелла, т. к. Максвелл теоретически решил задачу о распределении молекул идеального газа по скоростям поступательного движения.

Распределение Максвелла позволяет определить, какое число молекул DN из общего количества N молекул идеального газа обладает при данной температуре скоростями, лежащими в интервале от v до v + Dv. При этом Максвелл предполагал, что газ химически однороден и находится в состоянии термодинамического равновесия.

Закон распределения молекул по скоростям представлен на рисунке. По оси ординат отложена функция распределения молекул по скоростям

,

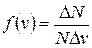определяющая относительное число молекул 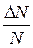из общего числа N молекул, скорости которых лежат в интервале от v до v + Dv.

Эта функция имеет максимум при значении

,

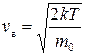называемом наиболее вероятной скоростью. Большинство молекул газа движется с наиболее вероятной скоростью, тогда как число молекул, имеющих очень малые и очень большие скорости, мало.

Площадь, ограниченная графиком функции и осью v, дает полное число молекул.

Закон распределения молекул по скоростям позволяет также подсчитать величину средней (средней арифметической) скорости 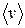поступательного движения молекул идеального газа. Ее можно найти, поделив сумму скоростей молекул на их число:

.

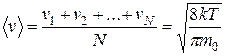Наконец, с помощью данного распределения можно найти среднюю квадратичную скорость. Так называется величина

,

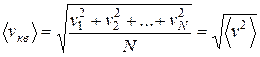т. е. квадратный корень из среднего значения квадрата скорости поступательного движения молекулы. Для вычисления 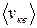надо скорость каждой молекулы возвести в квадрат, сложить полученные значения и сумму разделить на общее число молекул:

.

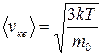Таким образом, существуют три скорости, характеризующие состояние газа – наиболее вероятная, средняя арифметическая и средняя квадратичная.

Отметим, что закон распределения Максвелла представляет собой статистический закон, полученный с помощью методов теории вероятностей, а потому тем более точный, чем большее число молекул N рассматривается. Важно подчеркнуть, что данный закон справедлив только для хаотического теплового движения молекул идеального газа.

Вопросы для самоконтроля:

1. Сформулируйте основные положения МКТ.

2. Что такое атом? молекула?

3. Что такое относительная молекулярная масса?

4. Что называется количеством вещества? Единица измерения.

5. Каков физический смысл постоянной Авогадро?

6. В чем измеряется молярная масса?

7. Назовите параметры состояния газа.

8. Какой газ называют идеальным?

9. Запишите основное уравнение МКТ газов.

10. Какова связь между кинетической энергией поступательного движения молекул газа и его температурой?

11. Запишите уравнение Менделеева-Клапейрона.

12. Сформулируйте законы Бойля - Мариотта, Гей-Люссака, Шарля.

13. Какими скоростями характеризуют движение молекул газа?