Мгновенная скорость

Средняя скорость частицы характеризует быстроту ее движения за конечный промежуток времени. Неограниченно уменьшая этот промежуток, мы придем к физической величине, характеризующей быстроту движения в данный момент времени. Такая величина называется мгновенной скоростью или просто скоростью:

.

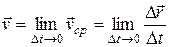Символ lim обозначает математическую операцию перехода к пределу. Под этим символом записывается условие, при котором выполняется данный предельный переход; в рассматриваемом случае это стремление к нулю промежутка времени Dt: Dt®0.

При вычислении скорости по этому правилу мы убедимся, что уменьшение промежутка времени Dt приводит к тому, что на некотором этапе получаемые очередные значения средней скорости будут все меньше и меньше отличаться друг от друга. Поэтому на практике при нахождении скорости можно остановиться на конечном значении Dt, достаточно малом для получения требуемой точности значения скорости.

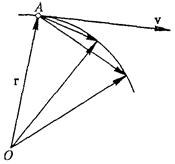Рассматриваемый предельный переход имеет ясный геометрический смысл. Поскольку вектор перемещения 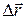направлен по хорде, соединяющей две точки траектории, то при сближении этих точек, происходящем при Dt®0, он принимает положение, соответствующее касательной к траектории в данной точке. Это значит, что вектор скорости направлен по касательной к траектории. Так будет в любой точке траектории. При прямолинейной траектории движения вектор скорости направлен вдоль этой прямой.

Аналогичным переходом определяется мгновенная скорость прохождения пути:

.

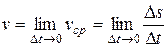Для плавной кривой, каковой является траектория любого непрерывного механического движения, длина дуги тем меньше отличается от длины стягивающей ее хорды, чем короче эта дуга. В пределе эти длины совпадают. Поэтому при Dt®0 можно считать, что Ds®Dr. Это означает, что скорость прохождения пути равна модулю мгновенной скорости.