Система отсчета. Траектория

Если рассмотреть явления, происходящие вблизи поверхности Земли, то мы убедимся в неравноценности различных направлений в пространстве. Так, тело, выпущенное из рук, всегда движется по вертикальному направлению вниз (примерно к центру Земли); свободная поверхность жидкости располагается в горизонтальной плоскости; для движения тела по вертикали вверх ему нужно сообщить начальную скорость, для движения же тела по вертикали вниз начальная скорость не нужна, и т. д. Эта неравноценность различных направлений в пространстве вызвана тем, что Земля притягивает к себе тела.

На весьма значительном расстоянии как от Земли, так и от других планет и звезд мы обнаружили бы, что в пространстве, свободном от больших тел, все направления равноценны. Мы говорим, что свободное пространство изотропно, т. е. в нем нет выделенных направлений, обладающих особыми свойствами.

Точно так же равноценны все точки пространства, если вблизи этих точек нет больших тел типа планет или звезд, Вследствие этого мы говорим, что свободное пространство однородно, т. е. в нем нет точек, обладающих особыми свойствами.

Наконец, однородным является также время. А именно, любые явления, происходящие в одних и тех же условиях, но в раз­ные моменты времени, протекают совершенно одинаково. Действительно, если сегодня маленький шарик падает с высоты 6 м за 1,1 с, то в этой же лаборатории с этой же высоты он падал столько же времени и месяц назад, и год назад, и столько же времени его па­дение будет продолжаться 1000 лет спустя.

Как мы убедимся далее, из факта однородности времени, однородности и изотропности пространства вытекает ряд важных следствий. Одно из них мы можем учесть уже сейчас: раз пространство однородно (т. е. все его точки равноценны) и изотропно (т. е. все направления в нем равноценны), то невозможно определить положение материальной точки относительно пространства.

Однако вполне возможно определить положение одного тела относительно другого. Например, положение лампочки в комнате полностью задается ее расстоянием от пола и расстояниями до двух взаимно перпендикулярных стен. С помощью такой же тройки чисел можно определить положение любого другого тела, находящегося как внутри комнаты, так и вне ее.

Системой отсчета называется тело или группа тел, которые в данной задаче рассматриваются как неподвижные и относительно которых определяется положение всех остальных тел.

В принципе любое тело может служить системой отсчета, однако не все системы отсчета могут оказаться одинаково удобными. 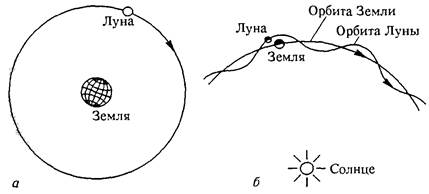Например, движение Луны относительно Земли (в так называемой геоцентрической системе отсчета) происходит по замкнутой почти круговой орбите (рис. а), но относительно Солнца (т. е. в гелиоцентрической системе отсчета) Луна движется по сложной незамкнутой орбите (рис. б).

В том, что одно и то же движение с точки зрения разных систем отсчета происходит по-разному, проявляется относительность механического движения. Вполне может возникнуть ситуация, когда некоторое тело движется в одной системе отсчета и покоится в другой.

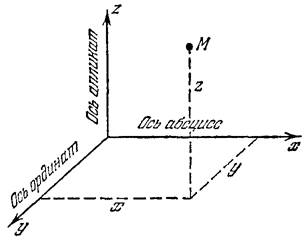С системой отсчета обычно связывают три взаимно перпендикулярные прямые оси координат. Положение точки характеризуется тремя координатами: абсциссой х, ординатой у и аппликатой z.

Движущаяся точка описывает в заданной системе отсчета линию, которая называется траекторией. Так, если зажечь прутик и быстро вращать его в воздухе, особенно в темной комнате, то отчетливо будет видна траектория движения уголька на конце прутика.

Форма траектории зависит от выбора системы отсчета. Действительно, пусть тело падает в вагоне, который движется относительно Земли. Тогда траектория этого тела относительно вагона будет прямой линией, относительно же Земли это будет кривая (при отсутствии сопротивления воздуха парабола). То же самое можно сказать о траектории, которую описывает какая-либо точка пропеллера движущегося самолета. В системе координат, связанной с самолетом, эта точка движется по окружности; в системе же координат, связанной с Землей, она движется по винтовой линии.

Таким образом, понятие формы траектории имеет относительный смысл. Нельзя говорить о форме траектории вообще; речь может идти лишь о форме траектории в заданной системе отсчета (системе координат).