Влияние ветра на путевую скорость и дальность полета
По отношению к летящему самолету ветер представляет собой переносное движение. При наличии ветра направление движения самолета относительно земной поверхности не совпадает с продольной осью самолета, т.е. ветер сносит самолет с того курса, каким этот самолет летит. Практически всегда самолет летит «немножко боком», и градус его поворота набок зависит от взаимного расположения направления полета и направления ветра, а также от скорости полета и скорости ветра. Пилоту воздушного судна еще до вылета необходимо знать, каким курсом и с какой скоростью нужно лететь, чтобы, выполняя полет в поле реального ветра, произвести посадку в заданное время на нужном аэродроме.
Все задачи, связанные с так называемым предварительным штурманским расчетом, выполняет экипаж самолета (обычно штурман) по исходным данным: маршрут и высота полета, время вылета и расчетное время посадки, направление и скорость ветра на эшелоне полета.
Задачи предварительного штурманского расчета помогает решить навигационный треугольник скоростей (рис. 7.1).
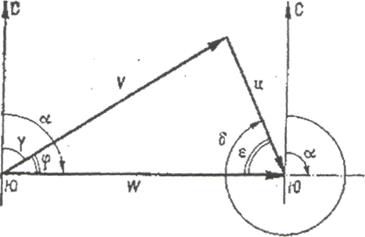
Рис. 7.1. Навигационный треугольник скоростей.
Навигационный треугольник скоростей составляют три вектора:
- вектор воздушной скорости V - вектор, показывающий, как перемещался бы (летел) самолет в неподвижном воздухе. Этот вектор направлен вдоль продольной оси самолета;
- вектор скорости ветра U - вектор, показывающий направление и скорость ветра в точке (районе), где находится самолет;
- вектор путевой скорости W вектор, показывающий полное (общее) перемещение самолета относительно земли под воздействием воздушной скорости и скорости ветра. Иными словами, путевая скорость представляет собой векторную сумму воздушной скорости и скорости ветра.
Для того чтобы навигационный треугольник скоростей был «рабочим», в этом треугольнике нужно также обозначить все необходимые углы. Такими углами являются:
- курс самолета g- угол между направлением на север и продольной осью самолета (вектором воздушной скорости);
путевой угол α - угол между направлением на север и вектором путевой скорости;
- угол сноса φ - угол между векторами воздушной и путевой скоростями.
Этот угол отсчитывается от вектора воздушной скорости вправо (плюсовой, по часовой стрелке) или влево (минусовой, против часовой стрелки) и показывает, насколько изменилось направление движения самолета под действием ветра.
Очевидно, что угол сноса равен
φ = α - g, (7.1)
- угол направления ветра, или просто направление ветра δ - угол между направлением на север и направлением вектора ветра (направлением, откуда дует ветер);
- угол ветра ε - угол между вектором ветра и вектором путевой скорости.
Он отсчитывается от вектора путевой скорости до вектора ветра по часовой стрелке и изменяется от 0 до 360°.
Есть еще один угол, о котором следует сказать, но который не входит в навигационный треугольник скоростей. Это курсовой угол ветра - угол между вектором воздушной скорости и вектором ветра. Он отсчитывается по часовой стрелке от вектора воздушной скорости и может изменяться от 0 до 360°. Курсовой угол ветра на практике анализируется сравнительно редко.
Элементы навигационного треугольника скоростей при полете самолета могут существенно изменяться вследствие большой пространственной и временной изменчивости ветра и большой протяженности многих маршрутов. Учет пространственной и временной изменчивости ветра особенно важен для воздушной навигации. Такой учет можно осуществлять, анализируя изменение основных элементов навигационного треугольника скоростей.
Из тригонометрии известно, что в каждом треугольнике отношение стороны к синусу противолежащего угла есть величина постоянная (теорема синусов).
В нашем случае (см. рис. 7.1) можно записать:
U/sin φ = V/sin ε (7.2)
или
sin φ = sin ε U/ V. (7.3)
Проанализируем последнее выражение. Из (7.3) видно, что снос самолета зависит от скорости полета, скорости ветра и угла ветра. Для простоты расчетов зададимся скоростью ветра U = 100 км/ч, скоростью полета V- 1000 км/ч и возьмем самые значимые значения для углов ветра.
Так, при ε = 0° (попутный ветер) sin ε = 0, а следовательно, и sin φ = 0, т.е. при строго попутном ветре никакого сноса самолета с курса нет. Аналогичная картина наблюдается и при ε = 180° (встречный ветер). Максимальный снос самолета с курса будет наблюдаться при строго боковом ветре (ε = 90 или 270°). В этом случае его можно определить по формуле (7.4), так как при ε = 90° и 180° sin ε по абсолютной величине равен единице:
φ = arcsin ( ±U/ V).(7.4)
Для принятых нами значений скорости ветра и скорости полета соотношение (U/ V)= 0.1, а следовательно, угол сноса φ = 6°. Из выражения (7.4) видно, что чем больше соотношение (U/ V), тем больше снос самолета. В табл. 7.1 приведены значения углов сноса самолета при разной скорости полета и различных скоростях ветра,
Таблица 7.1
ЗНАЧЕНИЯ УГЛОВ СНОСА САМОЛЕТА φ °) В ЗАВИСИМОСТИ ОТ СКОРОСТИ ПОЛЕТА И СКОРОСТИ ВЕТРА
| Тип ВС | V, км/ч | U, км/ч | ||
| Ил- 18 | 5,0 | 9,5 | 19,5 | |
| Ил-62 | 3,5 | 7,0 | 14,0 | |
| Ту- 144 | 3,0 | 6,0 |
Из табл. 7.1 видно, насколько большим может быть снос самолета даже при большой скорости полета.
Оценим связь между путевой скоростью, с одной стороны, и скоростью и направлением ветра - с другой. Из рис. 7.1 видно, что
W = V+U = Vcos φ + U cos ε. (7.5)
Этой формулой может пользоваться любой штурман. Путевой угол (откуда и куда летит самолет) штурман всегда хорошо знает, и, узнав на метеостанции ветер по маршруту, определяет угол ветра. Представим выражение (7.2) в несколько другом виде и обе части этого выражения возведем в квадрат. Тогда получим
U 2 sin 2 ε = V 2 sin 2 φ.
В окончательном виде можно записать, что
W= √ V2 - U 2 sin 2 ε + U cos ε. (7.6)
Из формулы видно, что при попутном ветре (ε = 0°) путевая скорость становится больше воздушной на величину скорости ветра (W = V + U), в данном случае никакого сноса ветра ненаблюдается. Строго встречный ветер (ε = 180°) уменьшает путевую скорость на величину скорости ветра (W = V-U), также без сноса самолета с курса, а строго боковой ветер (е = 90 или 270°) не только изменяет скорость полета, но и вызывает максимальный снос.
Информация о ветре на уровне полета используется не только для штурманских расчетов, но и для ввода в автоматические навигационные устройства и бортовые ЭВМ.
Дальность (L) и продолжительность (T) полета можно определить, если известны располагаемый запас топлива на самолете (GТ), а также его километровый (с к) и часовой расход (с h) по формуле:
L = GТ / с к , T = GТ / с h . (7.7)
Известно также, что часовой и километровый расходы топлива связаны (при наличии ветра) между собой соотношением:
с к = с h / W. (7.8)
Кроме того, простые логические рассуждения позволяют утверждать, что время полета и часовой расход топлива не зависят от ветра, а дальность полета и километровый расход топлива от ветра зависят. Действительно, если на самолете запас топлива на три часа полета, то при любом ветре самолет может три часа находиться в воздухе, какое бы расстояние он не пролетел. А километровый расход топлива от ветра зависит. Это хорошо видно из последнего выражения (7.8) - попутный ветер уменьшает километровый расход топлива, а встречный, наоборот, увеличивает.
При штиле километровый расход топлива и дальность полета могут быть рассчитаны по формулам (7.9):
с к ,0 = с h /V, L0 = GТ / с к ,0 = GТ V / с h = V T, (7.9)
а при наличии ветра - по формулам (7.10)
с к = с h / W, L = GТ / с к = GТ W / с h = W T. (7.10)
Если взять отношение L/ L0, то мы получим
L/ L0 = с к ,0 / с к = W /V = √ 1 - U 2 sin 2 ε/ V2 + U cos ε/ V . (7.11)
Таким образом, максимальная дальность полета, которая наблюдается при попутном ветре (ε = 0°), определяется выражением (7.12), а минимальная дальность (при встречном ветре ε = 180°) - выражением (7. 13):
(L/ L0)макс = 1+U/ V, (7.12)
(L/ L0) макс = 1 - U/ V. (7.13)
Дата добавления: 2020-12-11; просмотров: 1253;











