Предмет расположен на расстоянии больше радиуса кривизны. Изображение-действительное, уменьшенное, перевернутое.

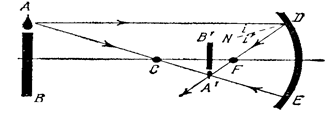
Рис. 12.

2) Предмет расположен на расстоянии, равном радиусу кривизны. Изображение - действительное, равно по величине размерам предмета, перевернутое, располагается строго под предметом.

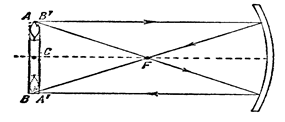
Рис. 13.

3) Предмет расположен между фокусом и полюсом зеркала. Изображение - мнимое, увеличенное, прямое .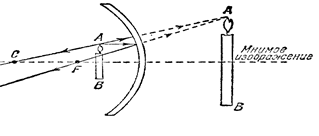

Рис. 14.

Выпуклое зеркало. Если пучок параллельных лучей падает на выпуклое зеркало, то после отражения продолжения лучей пересекаются в точке, называемой фокусом. Фокус выпуклого зеркала мнимый. Формула выпуклого зеркала

.

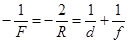Правило знаков для d и f остается таким же, как и для вогнутого зеркала.

Линейное увеличение предмета

.

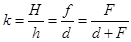Рассмотрим несколько примеров на построение изображений в выпуклых зеркалах.

1) Предмет расположен на расстоянии большем радиуса кривизны. Изображение мнимое, уменьшенное, прямое.

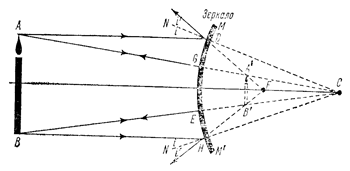
Рис. 15.

2) Предмет расположен на расстоянии, равном радиусу кривизны. Изображение мнимое, уменьшенное, прямое

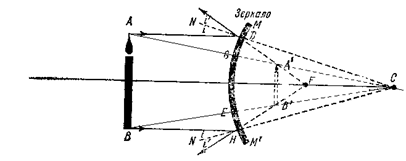
Рис. 16.

Таким образом, независимо от расположения предмета относительно выпуклого зеркала изображение оказывается всегда мнимым , прямым, уменьшенным и расположенным за зеркалом. В то время как изображения в вогнутом зеркале более разнообразны, зависят от расположения предмета относительно зеркала. Поэтому эти зеркала наиболее часто применяются в медицине.

Задача 2 На сферическое зеркало падает луч света. Найти построением ход луча после отражения в двух случаях :а) от вогнутого зеркала (рис. 17); б) от выпуклого зеркала (рис. 18). На рисунках О - полюс зеркала; С - оптический центр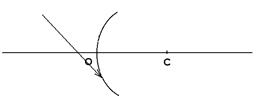

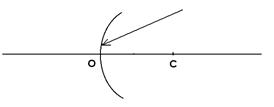
Рис. 17. Рис. 18.

Решение:

Параллельные пучки света после отражения от зеркала собираются в фокусе, поэтому параллельно заданному лучу проведем лучи: 1) проходящий через оптический центр зеркала С и 2) проходящий через полюс О (рис. 19). Эти лучи пересекутся в точке, которая является побочным фокусом Fпобоч, поэтому после отражения заданный луч также должен пройти через эту точку. Таким образом, мы определили ход луча после отражения от вогнутого зеркала.

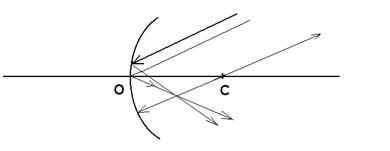
Рис. 19.

Самостоятельно постройте ход луча для случая б).

Задача 3 Точка S¢ является изображением точечного источника S в сферическом зеркале, оптическая ось которого N1N2 (рис. 20). Найти построением положение оптического центра зеркала С, фокуса F и полюса О.

Рис. 20.

Решение:

Воспользовавшись тем, что луч падающей на зеркало в его полюсе, отразится симметрично относительно главной оптической оси, построим симметричную с S точку S¢1 и проведем луч S¢S1 до пересечения с осью N1N2 в точке О (рис. 21). Эта точка и будет являться полюсом зеркала. Оптический центр С зеркала, очевидно, может быть найден как точка пересе­чения луча SS¢ c осью N1N2.Фокус найдется обычным построением луча SM, параллельного главной оптической оси, который, отразившись должен пройти через фокус F (лежащий на оптиче­ской оси зеркала) и через S¢.

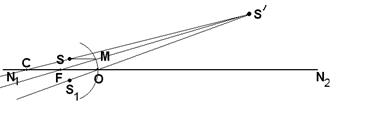
Рис. 21.

Данное зеркало вогнутое, т.к. дает изображение прямое, увеличенное, мнимое.

Задача 4 Зубному врачу требуется маленькое зеркало, которое на расстоянии 2,1 см от зуба давало бы прямое 5,5 кратное увеличение. Какое зеркало следует для этого взять, с каким радиусом кривизны?

Дано:

а=2,1 см

к=5,5

______

R=?

Решение:

Т.к. зеркало должно дать изображение прямое и 5,5 кратно увеличенное, то это вогнутое зеркало. Построим изображение, используя лучи: а) параллельный главной оптической оси АМ¢, после отражения он идет через фокус F; б) луч, идущий через оптический центр С, после отражения идет в том же направлении.

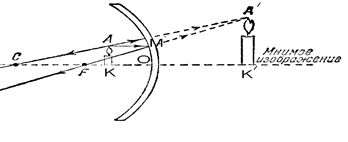
Рис. 22.

Т.к. лучи а) и б) расходятся, то изображение находится на продолжении этих лучей. Из формулы сферического зеркала

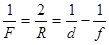
(f - в формулу входит со знаком минус, т.к. изображение мнимое) найдем радиус кривизны зеркала R

.

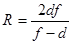
Из рис. 22 видно, что КО = d; ОК¢ = f, по условию задачи d + f = a, а линейное увеличение зеркала определяется соотношением

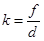
Т.к. величины а и k заданы по условию задачи, то из системы последних двух уравнений найдем d и f

; .

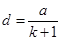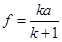Тогда

.

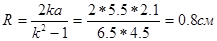Итак, врачу требуется вогнутое зеркало с радиусом кривизны R @1 см.

ПОСТРОЕНИЕ ИЗОБРАЖЕНИЙ В ЛИНЗАХ

Прозрачное тело, ограниченное двумя сферическими поверхностями, называется линзой.

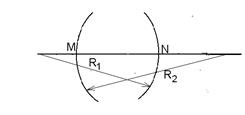
Рис. 23.

Прямую, на которой лежат центры сферических поверхностей, называют главной оптической осью линзы. Главная оптическая ось линзы пересекает сферические поверхности в точках М и N – это вершины линзы. Если расстоянием MN можно пренебречь по сравнению с R₁ и R₂, то линза называется тонкой. В этом случае (×)М совпадает с (×)N и тогда (×)М будет называться оптическим центром линзы. Все прямые, проходящие через оптический центр линзы, кроме главной оптической оси называются побочными оптическими осями.

Собирающие линзы. Фокусом собирающей линзы называется точка, в которой пересекаются параллельные лучи после преломления в линзе. Фокус собирающей линзы – действительный. Фокус, лежащий на главной оптической оси, называется главным фокусом. Плоскость, в которой лежат фокусы, называется фокальной плоскостью. Расстояние от центра линзы до главного фокуса называется главным фокусным расстоянием F.

Правила хода лучей в собирающей линзе:

1) луч, падающий на линзу параллельно какой-либо оптической оси, после преломления пройдет через фокус, лежащий на этой оптической оси

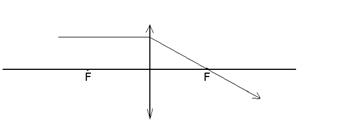
Рис. 24.

2) луч, идущий вдоль оптической оси, не меняет своего направления

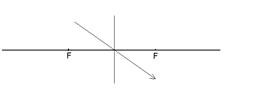
Рис. 25.

3) луч, проходящий через передний фокус, после преломления в линзе пойдет параллельно главной оптической оси

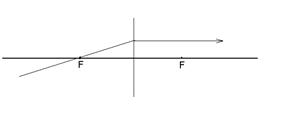
Рис. 26.

Формула собирающей линзы:

,

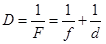где F - фокусное расстояние линзы; D - оптическая сила линзы; d - расстояние от предмета до центра линзы; f - расстояние от центра линзы до изображения. Правило знаков будет таким же, как и для зеркала.

Линейное увеличение, даваемое линзой,

,

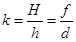где H - высота изображения; h - высота предмета.

Рассеивающие линзы. Лучи, падающие на рассеивающую линзу параллельным пучком, расходятся так, что их продолжения пересекаются в точке, называемой мнимым фокусом.

Правила хода лучей в рассеивающей линзе (рис. 27):

1) лучи, падающие на линзу параллельно какой-нибудь оптической оси, после преломления пойдут так, что их продолжения пройдут через фокус, лежащий на оптической оси;

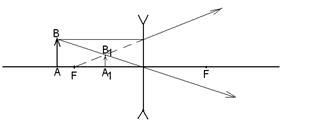
Рис. 27.

2) луч, идущий вдоль оптической оси, не меняет своего направления.

Формула рассеивающей линзы:

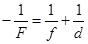
(правило знаков остается прежним).

Фокусное расстояние линзы определяется по формуле

,

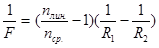где n_лин. - показатель преломления материала линзы, а n_ср. - показатель преломления среды, в которой находится линза; R₁, R₂- радиусы сферических поверхностей линзы.

Для выпуклой поверхности R берется со знаком « плюс», а для вогнутой – со знаком «минус», для плоской – R=¥.

Задача 5 Построить изображение светящейся точки, расположенной на главной оптической оси собирающей линзы (рис. 28).На рисунке: О - оптический центр линзы, F-ее главный фокус; S- светящаяся точка

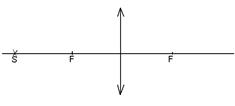
Рис. 28.

Решение:

Так как светящаяся точка S находится на главной оптической оси, то все три луча, используемые для построения изображения совпадают и идут вдоль главной оптической оси, а для построения изображения нужно минимум два луча. Поэтому для построения изображения делают дополнительное построение: 1) перпендикулярно главной оптической оси через точку F строят фокальную плоскость, 2) выбирают любой луч, идущий из точки S, 3) параллельно выбранному лучу, проводят побочную оптическую ось. Точка пересечения этой побочной оптической оси с фокальной плоскостью является побочным фокусом, поэтому выбранный нами луч после преломления линзой пройдет через эту точку. Точка пересечения преломленного луча с главной оптической осью и даст нам изображение точки S - S¢ (рис. 29).

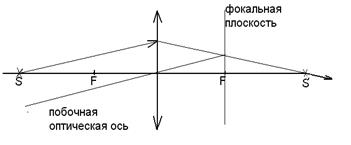
Рис. 29.

Задача 6 На тонкую линзу падает луч света. Найти построением ход луча после его преломления линзой: а) собирающей (рис. 30,а); б)рассеивающей (рис. 30,б). На рисунке: О - оптический центр линзы; F- главный фокус.

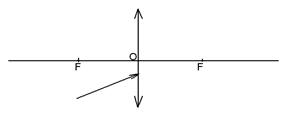
Рис. 30,а.

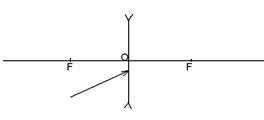
Рис. 30,б.

Решение:

Рассмотрим случай а). Построим фокальную плоскость. Параллельно заданному лучу проведем побочную оптическую ось до пересечения с фокальной плоскостью. Точка пересечения побочной оптической оси с фокальной плоскостью и является побочным фокусом. После преломления линзой луч должен пройти через эту точку (см. рис. 31).

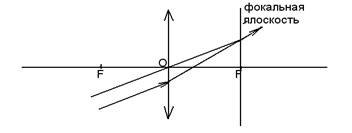
Рис. 31.

Самостоятельно постройте ход луча в рассеивающей линзе.

Задача 7 На заданной оптической оси N1N2 линзы найти построением оптический центр линзы и ее главные фокусы, если известно положение источника S и положение изображения S¢ (рис. 32)

Рис. 32.

Решение:

Центр линзы О – точка пересечения прямых SS¢ и N₁N₂. Фокусы легко находятся построением лучей, параллельных главной оптической оси (рис. 33)

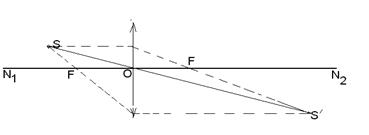
Рис. 33.

Задача 8 У дальнозоркого человека расстояние наилучшего зрения равно 100 см. Какую оптическую силу должны иметь его линзы, чтобы он мог читать газету с расстояния 25 см. Для простоты считать, что линзы очков располагаются вплотную к глазам.

Дано:

d = 25 см.=0.25 м.

F = 100 см = 1м

f-?

Решение:

Итак , мы хотим, чтобы расстояние от объекта (газеты) до линзы было 25 см. и при этом изображение должно оказаться на расстоянии 100 см.

Изображение и объект в этом случае располагаются по одну стороны от линзы, т.е. изображение является мнимым, поэтому в формуле линзы расстояние f = 100 см будет отрицательным (правило знаков)

,

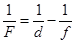а d = 25 см., тогда .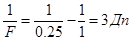

Оптическая сила линзы (очков) равна

.

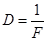Для данного дальнозоркого человека нужны очки с оптической силой в 3 диоптрии.

Пусть близорукости отвечает расстояние наилучшего зрения 12 см и предел зрения 17 см. Какую оптическую силу должны иметь очки, чтобы человек мог отчетливо видеть далекие предметы, и каким будет в этом случае расстояние наилучшего зрения? Предполагается, что линзы очков находятся на расстоянии 2,0 см от глаза.

Дано:

f = 17 см – 2 см = 0.15м

f₁ = 12 см - 2см = 0.1м

найти: D - ?

d₁ - ?

Решение:

Изображение удаленных предметов (d = ¥) должно находиться на расстоянии 17 см от глаза или 15 см перед линзой (f = -15 см):

,

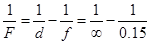отсюда F = -0,15 см, или D = 1/F = -6,7 Дп. Знак минус указывает на то, что линза должна быть рассеивающей. Расстоянию наилучшего зрения должно соответствовать изображение, находящееся на расстоянии 12 см от глаза или на расстоянии 10 см от линзы. Поэтому f₁ = -0,10 см и .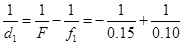

Отсюда d₁ = 30 см. Следовательно, когда близорукий человек наденет очки, его расстояние наилучшего зрения (до линзы) станет равным 30 см.

В последнем примере для коррекции зрения можно было бы использовать контактные линзы. Поскольку они помещаются непосредственно на роговицу, то в этом случае не нужно вычитать 2,0 см, и поэтому для удаленных объектов di = -17 см и D = 1/F = -5,9 Дп. Таким образом, при коррекции одного и того же дефекта зрения с помощью контактной линзы или очков их фокусные расстояния оказываются несколько разными из-за различия в расположении линзы относительно глаза.

Напоминаем, что расстояние до ближайшей точки, на которую глаз может четко фокусироваться, называется расстоянием наилучшего зрения.

ОСОБЕННОСТИ РЕШЕНИЯ ЗАДАЧ

Из приведенных выше примеров следует, что решение задач по геометрической оптике всегда следует начинать с выполнения построений. Причем следует помнить, что для построения изображения предмета достаточно найти изображение двух его крайних точек, поскольку в общем курсе физики рассматривают только такие зеркала и линзы, в которых всякая прямая линия преобразуется в прямую. Изображение точек предмета строят при помощи двух характерных лучей.

Это замечание относится не только к тем задачам, в которых следует выполнить только графическое построение, но и к задачам расчетного характера.

Все задачи геометрической оптики можно условно разделить на четыре группы.

К первой группе отнесем сравнительно немногочисленные задачи на построение изображений в плоском зеркале. Все построения сводятся к использованию закона отражения света. Определенных навыков решения требуют лишь задачи, связанные с построениями и расчетами в системах плоских зеркал. Принципиально такие задачи не отличаются от задач на одно зеркало, однако требуют для своего решения более умелого применения теорем из геометрии.

Ко второй группе отнесем задачи о преломлении света на плоской границе раздела двух сред, в частности задачи о прохождении света через плоскопараллельную пластинку и призму. Можно рекомендовать следующий порядок решения таких задач:

- сделать чертеж с указанием хода лучей, идущих из одной среды в другую; в точке падения луча на границу раздела двух сред провести нормаль к поверхности, отметить углы падения и преломления, указать стрелкой начальное направление луча; особое внимание обратить на оптическую плотность рассматриваемых сред и помнить, что при переходе луча света из оптически более плотной среды в менее плотную возможно явление полного внутреннего отражения;

- записать требуемую формулу для каждого перехода луча из одной среды в другую;

- составить вспомогательные уравнения, связывающие углы, расстояния (заданные в задаче и искомые), используя геометрические и тригонометрические соотношения;

- решить полученную систему уравнений относительно неизвестной величины.

К третьей группе отнесем задачи о построениях и расчетах изображений в одиночных сферических зеркалах и линзах.

Обычно студенты испытывают трудности при построении изображений точек, лежащих на главной оптической оси линзы (зеркала). Эти построения следует проводить с использованием побочной оптической оси. При этом рассматривают произвольный луч света, падающий на линзу (зеркало) под некоторым углом. Затем проводят побочную оптическую ось, параллельную рассматриваемому лучу, и находят побочный фокус линзы (зеркала). Он расположен в точке пересечения побочной оси с фокальной плоскостью.

В случае собирающей линзы рассматриваемый луч после преломления должен пройти через задний побочный фокус; в случае рассеивающей линзы продолжение рассматриваемого луча должно пройти через передний побочный фокус; в случае рассеивающей линзы продолжение рассматриваемого луча должно пройти через передний побочный фокус.

Можно рекомендовать следующий порядок решения задач третьей группы:

- построить изображение светящейся точки или предмета, указав на чертеже характерные точки линзы (зеркала ) О, F, 2F, расстояния d, f, F;

- записать уравнения, определяющие фокусное расстояния линзы (зеркала), обратив особое внимание на знаки перед слагаемыми в этих уравнениях, помня, что все расстояния до действительных точек надо брать со знаком плюс, а до мнимых со знаком минус;

- если записанных уравнений недостаточно для решения задачи. То следует добавить вспомогательные уравнения, отражающие дополнительные данные условия задачи; как правило, вспомогательные уравнения устанавливают связи между заданными и искомыми расстояниями; эти связи можно получить из анализа чертежа;

- решить систему основных и вспомогательных уравнений относительно искомой величины.

В четвертую группу входят задачи на расчет и построение изображений в различных оптических системах, состоящих из нескольких линз (зеркал) или линз и зеркал и т.д.

Задачи этой группы следует решать по такой схеме:

- сделать схематический чертеж, соответствующий условию задачи; отметить на нем линзы, зеркала и другие системы, изменяющие ход светового луча, а также отметить характерные точки линз (зеркал) и заданные расстояния;

- построить изображение предмета в первой линзе (зеркале), считая, что вторая линза (зеркало) отсутствует;

- используя основные уравнения для линзы (зеркала) и, если требуется определить размеры изображения, то вначале нужно найти расстояние от этого изображения до первой, а затем и до второй линз; при этом настоятельно рекомендуется сразу же находить числовые значения этих расстояний, так как это дает возможность судить о конкретном расположении изображения относительно второй линзы (зеркала);

- считая первое изображение предметом для второй линзы (зеркала), аналогично находят построением положение и размер второго изображения ;

- вновь записывают уравнения для второй линзы (зеркала);

из условия задачи или анализа чертежа к записанным уравнениям добавляют вспомогательные уравнения связи между различными расстояниями;

- получив полную систему уравнений, решить ее относительно искомых величин.

Обратим внимание на существенную деталь. При построении и расчетах всегда следует различать случаи. Когда на вторую линзу (зеркало) лучи падают сходящимся или расходящимся пучком. В первом случае изображение точки нужно рассматривать как мнимый предмет для второй линзы (зеркала), во втором – как действительный.

Задачи для самостоятельной работы:

Задача 1.

Может ли рассеивающая линза при каких-либо условиях создавать действительное изображение? Объясните.

Задача 2.

Будет ли близорукий человек, носящий очки для коррекции зрения, отчетливо видеть с ними под водой? Свой ответ (утвердительный или отрицательный) поясните, построив ход лучей.

Задачи для индивидуальной работы:

1.1Луч света падает под углом a=60° на стеклянную пластинку толщиной d = 30 мм. Определить боковое смещение луча после выхода из пластинки.

1.2На столе лежит лист бумаги. Луч света, падающий на бумагу под углом a = 30°, дает на ней светлое пятно. На сколько сместится это пятно, если на бумагу положить плоскопараллельную стеклянную пластинку толщиной d = 5 см?

1.3Пучок параллельных лучей падает на стеклянную пластинку под углом a = 60°, и преломляясь переходит в стекло. Ширина пучка в воздухе равна 10 см. Определить ширину пучка в стекле.

1.4Узкий параллельный пучок света падает на плоскопараллельную стеклянную пластинку под углом a, синус которого равен 0,8. Вышедший из пластинки пучок оказался смещенным относительно продолжения падающего пучка на расстояние d = 2 см. Какова толщина h пластинки, если показатель преломления стекла n = 1.7?

1.5Луч света выходит из скипидара в воздух. Предельный угол полного внутреннего отражения для этого луча равен 42°23¢. Чему равна скорость распространения света в скипидаре?

1.6Определить показатель преломления n скипидара и скорость распространения света v в скипидаре, если известно, что при угле a = 45° угол преломления b = 30°.

1.7Определить предельный угол полного внутреннего отражения для алмаза в воздухе и в воде.

1.8Предельный угол полного внутреннего отражения на границе стекло-жидкость i = 70°. Чему равен показатель преломления жидкости n, если у стекла показатель преломления равен 1,60?

1.9Луч света переходит из среды с показателем преломления n1 в среду с показателем преломления n2. Показать, что если угол между отраженным и преломленным лучами равен p/2, то выполняется условие tqa = n2/n1 (a-угол падения).

1.10На дне водоема глубиной 80 см находится точечный источник света. Определить диаметр освещенного круга на поверхности воды.

1.11На стакан, наполненный водой положена стеклянная пластинка. Под каким углом должен падать на пластинку луч света, чтобы от поверхности раздела воды со стеклом произошло полное внутреннее отражение? Показатель преломления стекла равен 1,5.

1.12На дно сосуда, наполненного водой до высоты в 10 см, помещен источник света. На поверхности воды плавает круглая непрозрачная пластинка таким образом, что ее центр находится над источником света. Какой наименьший радиус должна иметь эта пластинка, чтобы ни один луч не мог выйти через поверхность воды?

1.13В водоем на некоторую глубину помещают точечный источник белого света. Показатели преломления воды для красных и фиолетовых лучей соответственно равны 1,328 и 1,335. Вычислить отношение радиусов кругов, в пределах которых возможен выход красных и фиолетовых лучей в воздух.

1.14Плоское зеркало поворачивается на угол a = 27°. На какой угол b повернется отраженный от зеркала луч?

1.15Человек высотой 1,5 м, стоящий на берегу озера, видит. Луну в небе по направлению, составляющему угол a = 60° с горизонтом. На каком расстоянии от себя человек видит отражение Луны в озере?

1.16На горизонтальном дне водоема глубиной h = 1,2 м лежит плоское зеркало. На каком расстоянии от места вхождения луча в воду этот луч снова выйдет на поверхность воды после отражения от зеркала? Угол падения луча a=30°, показатель преломления воды равен 1,33.

1.17Человек ростом h = 1,75 м находится от столба на расстоянии 6м. На каком расстоянии от себя он должен положить горизонтально на землю зеркало, чтобы видеть верхушку столба? Высота столба 7м.

1.18Объяснить, почему в лунную ночь на поверхности моря видна лунная дорожка, а не изображение лунного диска.

1.19Вогнутое сферическое зеркало имеет фокусное расстояние F = 1 м. На каком расстоянии d от зеркала необходимо поместить источник света, чтобы его изображение совпало с самим источником?

1.20Расстояние светящейся точки от вогнутого зеркала равно двум радиусам кривизны. Светящаяся точка находится на главной оптической оси зеркала. Где расположено изображение точки? Построить это изображение.

1.21На вогнутое зеркало падает луч АОВ, пересекающий главную оптическую ось зеркала в точке О. Отраженный от зеркала луч ВО1D пересекает ту же ось в точке О1 (см. рис.). Найти построением положение фокуса зеркала.

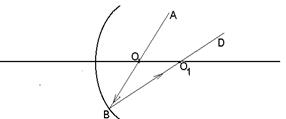
Рис. к задаче 1.21.

1.22С помощью вогнутого зеркала получено действительное изображение предмета с увеличением k1 = 5. Оказалось, что если переместить предмет на некоторое расстояние вдоль оптической оси, изображение переместится вдоль оптической оси на такое же расстояние. Найти полученное при новом расположении увеличение k2.

1.23Фокус вогнутого зеркала расположен на расстоянии а = 0,24 м от светящегося предмета и на расстоянии b = 0,54 м от его изображения. Найти увеличение k предмета, даваемое зеркалом.

1.24Каков радиус кривизны R вогнутого сферического зеркала ,если изображение предмета, помещенного на расстоянии d = 21 см, получается в k = 6 раз больше самого предмета?

1.25Вогнутое сферическое зеркало дает на экране изображение предмета, увеличенное в 4 раза. Расстояние от предмета до зеркала равно 25 см. Определить радиус кривизны зеркала.

1.26Фокусное расстояние вогнутого зеркала равно 15 см. Зеркало дает действительное изображение предмета, уменьшенное в три раза. Определить расстояние от предмета до зеркала.

1.27Радиус кривизны выпуклого зеркала равен 50 см. Предмет высотой 15 см находится на расстоянии, равном 1 м, от зеркала. Определить расстояние от зеркала до изображения и его высоту.

1.28Радиус вогнутого зеркала – R. На главной оптической оси этого зеркала помещен точечный источник света S на расстоянии d от зеркала. На каком расстоянии от вогнутого зеркала нужно поставить плоское зеркало, чтобы лучи, отраженные вогнутым, а затем плоским зеркалом, вернулись в точку S.

1.29Радиус кривизны вогнутого зеркала R = 90 см. Найти положение предмета, при котором его изображение будет действительным и увеличенным в три раза. Где должен находиться предмет, чтобы его изображение было мнимым и увеличенным в три раза?

1.30Точка А есть изображение точечного источника S в сферическом зеркале, оптическая ось которого N₁N₂. Найти построением положение центра зеркала и его фокуса (см. рис).

Рис. к задаче 1.30.

1.31SN – предмет, S¢N¢- его мнимое изображение в сферическом зеркале. NN¢- оптическая ось зеркала (см. рис.) Найти построением положение полюса зеркала, его центра и фокуса.

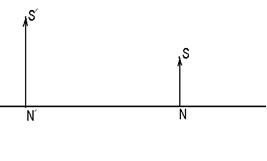
Рис. к задаче 1.31.

1.32Построить изображение S¢ светящейся точки S, находящейся на главной оптической оси выпуклого зеркала. Положение центра зеркала О, его полюса Р и его фокуса F известно.

1.33На каком расстоянии d от выпуклого зеркала нужно поместить источник света, чтобы его изображение получилось на расстоянии f = 60 см от зеркала? Главное фокусное расстояние зеркала F = 90 см.

1.34Во сколько раз высота изображения пламени свечи, удаленной на d = 1,5 м от выпуклого зеркала (F = 0,5 м) меньше высоты самого пламени?

1.35Выпуклое автомобильное зеркало заднего обзора имеет фокусное расстояние 45 см. Автомобиль находится на расстоянии 9м от этого зеркала. На каком расстоянии от зеркала получается изображение? Будет ли оно перед зеркалом или за ним?

1.36Из стекла требуется изготовить плосковыпуклую линзу, оптическая сила которой равна 5 дп. Определить радиус кривизны выпуклой поверхности линзы.

1.37При съемке автомобиля длиной l = 4 м пленка располагалась от объектива на расстоянии f = 60 мм. С какого расстояния d снимали автомобиль, если длина его негативного изображения L = 32 мм?

1.38Проверяя свои очки, учащийся получил на полу комнаты действительное изображение лампы, висящей на высоте Н = 3 м, держа очковое стекло под лампой на расстоянии h = 1м от пола. Какова оптическая сила D стекла?

1.39На рис. S - точечный источник света, S¢- его изображение. Определить построением положение оптического центра линзы каждого из ее главных фокусов в случаях, когда главной оптической осью является: 1) прямая М₁N₁; 2) прямая М₂N₂; 3) прямая М₃N₃; 4) прямая М₄N₄
Рис. к задаче 1.39.

1.40Из двух часовых стекол с одинаковыми радиусами кривизны, равными 0,5 м, склеена двояковогнутая «воздушная» линза. Какой оптической силой будет обладать такая линза в воде?

1.41Найти построением положение главных фокусов линзы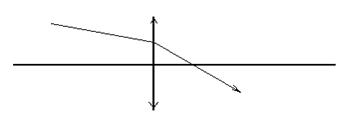
Рис. к задаче 1.41.

1.42Построить изображение отрезка АВ, параллельного главной оптической оси собирающей линзы (см. рис.)

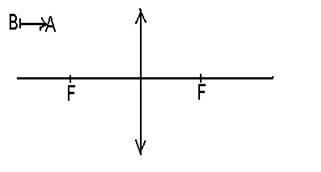
рис. к задаче 1.42.

1.43Построить изображение точки, лежащей на главной оптической оси собирающей линзы на расстоянии меньше фокусного. Положение фокусов линзы задано.

1.44 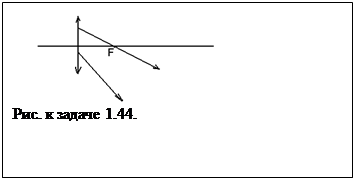Найти построением положение светящейся точки, если известен ход двух лучей после их преломления в линзе (см. рис.) Один из лучей пересекается с главной оптической осью линзы в ее фокусе.

1.45Линза изготовлена из стекла, показатель преломления которого для красных лучей n_кр. = 1,50, для фиолетовых лучей n_ф = 1,52. Радиусы кривизны обеих поверхностей линзы одинаковы и равны 1 м. Определить расстояние между фокусами линзы для красных и фиолетовых лучей.

1.46На расстоянии 40 см перед линзой (двояковыпуклой) на оптической оси находится светящаяся точка. Найти положение изображения этой точки, если она испускает монохроматический свет с длиной волны 1) l₁ = 7,6×10-5 см 2) l₂ = 4,3×10-5 см. Показатель преломления для красного и фиолетового лучей соответственно равны 1,5 и 1,8. Радиусы кривизны линзы R₁ = R₂ = 8 см.

1.47Предмет находится на расстоянии 10 см от переднего фокуса собирающей линзы, а экран, на котором получается четкое изображение предмета расположен за задним фокусом линзы на расстоянии 40 см от него. Найти оптическую силу линзы и увеличение предмета.

1.48В фокальной плоскости двояковыпуклой линзы расположено зеркало. Предмет находится перед линзой между фокусом и двойным фокусным расстоянием. Построить изображение предмета.

1.49Точечный источник света помещен на оптической оси собирающей линзы с фокусным расстоянием 0,2 м на расстоянии 0,5 м от нее. По другую сторону линзы в ее фокальной плоскости помещена рассеивающая линза. Каким должно быть фокусное расстояние рассеивающей линзы, чтобы мнимое изображение в ней источника совпало с самим источником?

1.50У линзы, находящейся в воздухе, фокусное расстояние равно 5 см, а у погруженной в раствор сахара 35 см. Определить показатель преломления раствора.