Лабораторная работа №1
ОПРЕДЕЛЕНИЕ ПОКАЗАТЕЛЯ ПРЕЛОМЛЕНИЯ ЖИДКОСТИ
РЕФРАКТОМЕТРОМ
Приборы и принадлежности: рефрактометр РПЛ-3, пипетка, растворы соли или сахара различной концентрации.
Цель работы: изучение принципа работы рефрактометра и исследование зависимости показателя преломления раствора от концентрации.
Краткая теория
При переходе света через границу раздела двух сред, скорость распространения света в которых различна, происходит изменение его направления. Это явление называется преломлением или рефракцией света. Абсолютным показателем преломления среды называют отношение скорости распространения света в вакууме с к скорости его распространения в данной среде v
n = c/v.
При переходе света из среды с меньшим показателем преломления (оптически менее плотная среда) в среду с большим показателем преломления (оптически более плотная среда) угол падения луча больше угла преломления. Если луч падает на границу раздела сред под наибольшим возможным углом i=p/2 (луч скользит вдоль границы раздела сред), то он будет преломляться под углом rпр < p/2. Этот угол является наибольшим углом преломления для данных сред и называется предельным углом преломления. Из закона преломления света следует
n12 = sin(p/2)/sin(rпр) = 1/sin(rпр) = n2/n1, (1)
где n1 и n2 - абсолютные показатели преломления сред, откуда sin(rпр) = n1/n2.
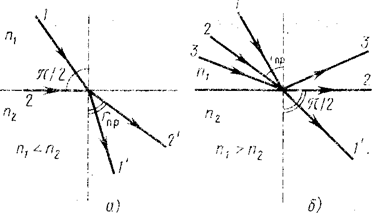 Рис.1.
Рис.1.
|
Если свет переходит из оптически более плотной среды в оптически менее плотную, то угол преломления больше угла падения. При некотором угле падения i луча угол преломления равен p/2, т. е. преломленный луч скользит вдоль границы раздела сред (рис. 1).
При дальнейшем увеличении угла падения преломление не происходит, весь падающий свет отражается от границы раздела сред. Угол i называется предельным углом полного внутреннего отражения и обозначается iпр.. Так как
n12 = sin(iпр)/sin(p/2) = n2/n1,
то
sin(iпр) = n2/n1. (2)
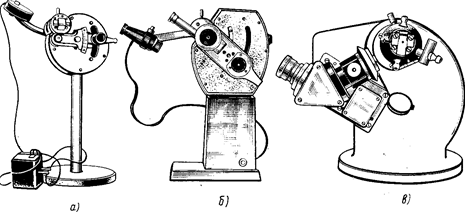 |
Рис.2.
 Таким образом, предельный угол преломления и предельный угол полного внутреннего отражения для данных сред зависят от их показателей преломления. Это нашло применение в приборах для измерения показателя преломления веществ — рефрактометрах (рис. 2, а-в), используемых при определении чистоты воды, концентрации общего белка сыворотки крови, для идентификации различных веществ и т. д.
Таким образом, предельный угол преломления и предельный угол полного внутреннего отражения для данных сред зависят от их показателей преломления. Это нашло применение в приборах для измерения показателя преломления веществ — рефрактометрах (рис. 2, а-в), используемых при определении чистоты воды, концентрации общего белка сыворотки крови, для идентификации различных веществ и т. д.
 Описание установки. Определение показателя преломления можно проводить различными способами: по измерению углов падения и преломления, по измерению наименьшего угла отклонения призмы и ее преломляющего угла, интерференционными методами (по
Описание установки. Определение показателя преломления можно проводить различными способами: по измерению углов падения и преломления, по измерению наименьшего угла отклонения призмы и ее преломляющего угла, интерференционными методами (по
смещению интерференционных полос), по смещению изображения предмета, рассматриваемого через плоскопараллельную пластинку с помощью микроскопа, иммерсионными методами и методами, основанными на полном отражении.
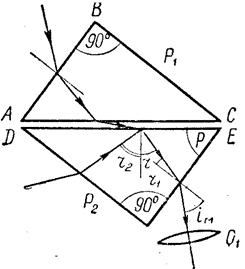
В работе применяется рефрактометр, в котором используется полное внутреннее отражение (рефрактометр Аббе). В рефрактометрах этого типа исследуемая среда (обычно жидкость) помещается в зазоре (около 0,1 мм) между гранями двух стеклянных прямоугольных призм (рис. 3). При измерениях используются два метода: метод скользящего луча и метод полного внутреннего отражения. При методе скользящего луча свет направляется через грань АВ призмы P1, проходит через матовую поверхность АС и далее через слой жидкости проникает в призму P2. Для лучей, которые скользят вдоль грани DE, можно записать закон преломления в виде:
n=n1 sin (r) (3)
Угол r равен предельному углу преломления для границы стекло - исследуемое вещество; n- показатель преломления исследуемой среды в зазоре; n1 - показатель преломления стекла призмы, n1 > n. Для грани EF закон преломления записывается в виде
n1sin (r1)= sin(iм). (4)
Преломляющий угол призмы DEF:
Р= г + г1. (5)
Тогда, учитывая (3),(4),(5), найдем:
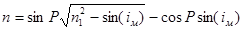 . (6)
. (6)
Угол выхода лучей iм будет иметь наименьшее значение для скользящих лучей. Лучи, проходящие через грань EF, будут выходить под углами от 90° до iм, определяемого соотношением (6). Если на пути этих лучей поставить собирающую линзу O1, то в ее фокальной плоскости получается изображение, на котором будет видна резкая граница между светом и тенью. Граница раздела соответствует направлению выхода лучей под наименьшим углом (т. е. под углом iм). Положение ее будет зависеть от величины показателя преломления среды (при данных призмах). Граница рассматривается через вторую линзу, которая совместно с O1 образует зрительную трубу, установленную на бесконечность. С помощью такой трубы определяется угол iм и по известным значениям Р и n1 рассчитывается показатель преломления.
При методе полного внутреннего отражения свет вводится в рефрактометр через матовую грань DF призмы P2. Свет падает на грань DE под всевозможными углами. При углах падениях r2 > r будет полное внутреннее отражение. Лучи, проходящие через грань EF и имеющие углы выхода больше iм, будут в фокальной плоскости давать изображение с меньшей освещенностью; лучи с углами выхода меньше iм (что соответствует условию г2 > r) будут давать большую освещенность. В поле зрения трубы в этом случае будет наблюдаться резкая граница раздела между полутенью и светом. Если при использовании первого способа верхняя часть поля зрения будет темной, то во втором способе эта часть поля будет иметь большую освещенность. Положение границы раздела в обоих случаях определяется условием (6). Вторым способом можно измерять показатель преломления и непрозрачных тел.
При освещении призм белым светом граница раздела будет размыта и окрашена в различные цвета. Чтобы получить резкое изображение, перед объективом зрительной трубы помещаются две призмы прямого зрения (призмы Амичи); каждая призма состоит из трех склеенных призм с различными показателями преломления и различной дисперсией (например, крайние призмы изготовлены из кронгласа, средняя - из флинтгласа). Призмы рассчитаны так, чтобы монохроматический луч с длиной волны 589,3 нм не испытывал отклонения. Такое устройство называется компенсатором.
При положении призм компенсатора, указанном на рисунке 4., их дисперсия равна нулю; при повороте одной из призм на 180° дисперсия будет равна удвоенному значению дисперсии одной призмы (при равных дисперсиях призм). В зависимости от взаимной ориентации призм дисперсию можно изменять от нуля до максимального значения. Поворотом призм компенсатора с помощью специального устройства добиваются резкого изображения границы, положение которой соответствует значению показателя преломления для желтой линии натрия (589,3 нм). В простых конструкциях рефрактометров в качестве компенсатора используется одна призма прямого зрения.
Схематически ход лучей в рефрактометре Аббе представлен на рисунке 4., где указано: 1- осветительное зеркало; 2 - откидная призма; 3 - основная призма; 4 - матовая грань; 5- исследуемое вещество; 6 - призма компенсатора; 7 - объектив трубы; 8 - оборотная призма; 9 - окуляр с отсчетной шкалой, расположенной в фокальной плоскости окуляра. Общий вид рефрактометра типа РПЛ-3 показан на рисунке 5. Обозначения те же самые, что на рисунке 4.
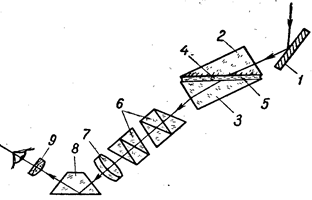
Рис.4. 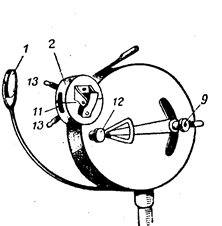
Рис.5.
Для удобства измерений шкала отградуирована непосредственно в значениях показателя преломления. В указанной конструкции рефрактометра имеется два окна, что позволяет вести измерения обоими способами. Одно из окон при измерениях закрывается шторкой 11; для установки компенсатора служит барабан 12. В оправе призм сделана камера, через которую может прокачиваться жидкость для поддержания постоянной температуры. Подача охлаждающей жидкости осуществляется через штуцеры 13. Перед началом работы необходимо проверить установку прибора. Для этой цели между призмами 2 и 3 помещается капля дистиллированной воды. Смещая окуляр в тубусе трубы, добиваются четкого изображения шкалы и визирной линии. Поворотом компенсатора добиваются четкого изображения границы. Далее, зрительную трубу перемещают до совпадения визирной линии с границей раздела. При правильной установке показание прибора должно быть равно 1,333 (при 20° С).
При измерении показателя преломления твердых тел исследуемый образец должен иметь полированную плоскость. Этой плоскостью он прижимается к призме P2 (откидная призма отводится при этом в сторону). Для обеспечения оптического контакта между соприкасающимися поверхностями вводится тонкий слой жидкости, показатель преломления которой nж < nтт (nтт — показатель преломления твердого тела).
Порядок выполнения работы
1. Подготовка прибора к работе:
a) откиньте верхнюю призму рефрактометра и пипеткой нанесите на нижнюю призму 2 - 3 капли дистиллированной воды. Опустите верхнюю призму;
б) фокусируя окуляр, получите резкие изображения поля зрения, визира и шкалы;
в) перемещая зрительную трубу, получите в поле зрения границу свет-тень. Линия раздела должна быть резкой и без цветной окраски. Последнее достигается поворотом рукоятки компенсатора;
г) совместите визир с границей раздела свет-тень. При правильной настройке рефрактометра показание шкалы при этом должно соответствовать показателю преломления воды n = 1,333 (при 20°С).
2. Исследование зависимости показателя преломления раствора NaCI или глюкозы от концентрации:
а) расположите источник света так, чтобы наблюдения проводились в проходящем свете;
б) измерьте показатели преломления раствора NaCI различной концентрации С. Для этого на нижнюю призму нанеся поочередно растворы различной концентрации и, совмещая визир с границей раздела свет-тень, определите по шкале показатели преломления растворов. Для каждого раствора измерение показателя преломления произведите несколько раз и найдите среднее значение <n>.
в) результаты измерений занесите в табл. 1;
г) постройте график зависимости показателя преломления от концентрации n = f(C);
д) используя метод наименьших квадратов постройте график линейной зависимости n = aCi + b;
е) измерьте показатель преломления раствора неизвестной концентрации. Определите по графику концентрацию Сx этого раствора;
ж) найдите по графику погрешность DСx измерения концентрации раствора.
Таблица 1.
| Концентрация раствора | |||||
| Показатель преломления | |||||
| <n> |
3. Измерение зависимости показателя преломления раствора NaCI или глюкозы от концентрации в отраженном свете:
а) расположите источник света так, чтобы наблюдения проводились в отраженном свете;
б) измерьте показатели преломления раствора NaCI различной концентрации С. Для каждого раствора измерение показателя преломления произведите несколько раз и найдите среднее значение <n>.
Таблица 2.
| Концентрация раствора | |||||
| Показатель преломления | |||||
| <n> |
в) результаты измерений занесите в табл. 2;
г) нанесите результаты на график зависимости показателя преломления от концентрации n = f(C), полученный ранее. Сравните результаты измерений обоими методами.
Таблица 3.
| Жидкость | Вода | Спирт | Глицерин | Вазелин | |
| Показатель преломления | |||||
| <n> |
4. Измерение показателей преломления различных жидкостей
а) измерить показатели преломления различных жидкостей, прилагаемых к прибору
б) результаты измерений занесите в табл. 3
в) расчитать погрешность измерений
Вопросы и упражнения
1. Сформулируйте законы отражения и преломления света.
2. Что называется предельным углом преломления?
3. В чем заключается явление полного внутреннего отражения?
4. Что называется предельным углам полного внутреннего отражения?
5. Опишите устройство рефрактометра Аббе.
6. Начертить ход лучей в измерительных призмах при работе методом скользящего луча и методом полного внутреннего отражения.
7. С какой целью применяется рефрактометр в медико-биологических исследованиях?
8. Каким образом проводится измерение показателя преломления жидких и твердых тел?
9. Определите, при каком угле падения луч, отраженный от границы раздела двух сред перпендикулярен преломленному лучу.
10. Найдите показатель преломления среды, если луч, преломленный на границе этой среды с воздухом перпендикулярен отраженному, а синус угла падения равен 0,73.
МЕТОД НАИМЕНЬШИХ КВАДРАТОВ
Если в результате многократных (i=1,2,…n) измерений некоторых величин х и y получается линейная система уравнений, каждое из которых имеет в вид
yi=ax i + b (1),
где xi и yi – результаты i-го измерения величин x и y, то можно попытаться определить коэффициенты линейной зависимости a и h.
Система уравнений (1), строго говоря, будет несовместной, так как результаты измерений x и y неизбежно содержат погрешности. Поэтому из этих уравнений можно определить не сами величины a и b а лишь их оценки, которые мы обозначим как A и B. Рассмотрим наиболее простой случай, когда величины x и y измеряются непосредственно, и все пары xi и yi имеют одинаковый вес (т.е. вклад каждой пары реализуется с одинаковыми вероятностями), случайными и систематическими погрешностями результатов измерения xi можно пренебречь. Кроме того, пусть случайные погрешности Dyi всех yi распределены по нормальному закону (распределение Гаусса) с одним и тем же стандартным отклонением sy, а систематическими погрешностями yi можно пренебречь.
Таблица 1. Зависимость величины y от x
| № | 
| 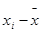
| 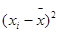
| 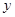
| 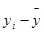
| 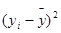
| 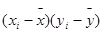
|
| 0,2 | -0,9 | 0,81 | 0,31 | -1,36 | 1,85 | 1,22 | |
| 0,4 | -0,7 | 0,49 | 0,59 | -1,08 | 1,17 | 0,76 | |
| 0,6 | -0,5 | 0,25 | 0,82 | -0,85 | 0,72 | 0,42 | |
| 0,8 | -0,3 | 0,09 | 1,17 | -0,50 | 0,25 | 0,15 | |
| 1,0 | -0,1 | 0,01 | 1,55 | -0,12 | 0,01 | 0,01 | |
| 1,2 | 0,1 | 0,01 | 1,87 | 0,20 | 0,04 | 0,02 | |
| 1,4 | 0,3 | 0,09 | 2,20 | 0,53 | 0,28 | 0,16 | |
| 1,6 | 0,5 | 0,25 | 2,35 | 0,68 | 0,46 | 0,34 | |
| 1,8 | 0,7 | 0,49 | 2,65 | 0,98 | 0,96 | 0,69 | |
| 2,0 | 0,9 | 0,81 | 3,20 | 1,53 | 2,44 | 1,38 |
Для наглядного понимания дальнейшего изложения представим все экспериментальные данные xi и yi в таблице 1 и на графике 1. Геометрически задача нахождения a и b состоит в определении параметров некоторой прямой: значения ординаты при нулевом значении абциссы и тангенса угла наклона, соответственно. Так как экспериментальные точки разбросаны и не лежат на графике на одной прямой, то апроксимирующих прямых можно провести бесконечно много. Задача экспериментатора – провести одну прямую, причем наилучшим образом. Такая прямая характеризуется наиболее точными оценками коэффициентов a и b, в том смысле, что они наиболее вероятные.
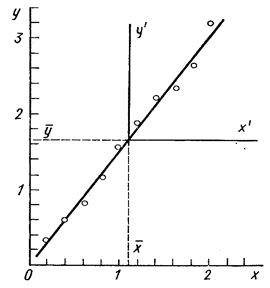
Рис.1. Построение прямой по данным совместных измерений методом наименьших квадратов
Можно доказать (доказательство выходит за рамки математических возможностей студентов-медиков), что оценки коэффициентов a и b будут наиболее вероятными, а аппроксимирующая прямая будет наилучшей, если сумма квадратов разностей Dyi=yi - (Axi+B) будет минимальна, т.е.
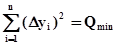 (2)
(2)
Условие минимальности (экстремальности) достигается, когда обращаются в ноль первые частные производные:
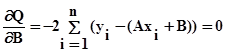 (3)
(3)
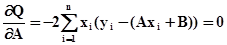 (4)
(4)
Отсюда находим
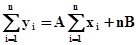 (5)
(5)
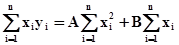 . (6)
. (6)
Решая эту систему относительно A и B, определим формулы для их вычисления:
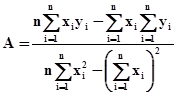 , (7)
, (7)
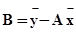 , (8)
, (8)
где 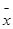 и
и 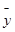 определяются соответственно как
определяются соответственно как
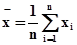 и
и 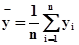 . (9)
. (9)
Формула (7) зачастую приводит к большим числам, работа с которыми усложняет вычисления. Поэтому для ее упрощения сделаем замену переменных
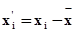 ;
; 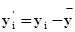 , (10)
, (10)
которая соответствует переносу начала координат в точку с координатами 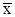 и
и 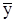 (центр тяжести прямой), через которую проходит искомая прямая. В новых переменных формула (7) принимает вид
(центр тяжести прямой), через которую проходит искомая прямая. В новых переменных формула (7) принимает вид
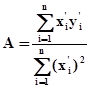 . (11)
. (11)
Возвращаясь к первоначальным координатам, получим
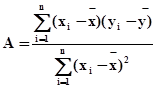 . (12)
. (12)
Таким образом, формулы (8) и (12) совместно с (9) позволяют определить оценки A и B. Что же касается погрешностей этих оценок, то в учебных лабораторных работах вполне достаточно вычислить либо оценку стандартного отклонения коэффициента A, либо доверительный интервал для a (интервал, в котором с установленной вероятностью может находиться искомый коэффициент a.
Оценка стандартного отклонения коэффициента A выражается следующим образом
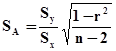 (13)
(13)
здесь использованы обозначения:
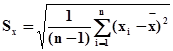 ; (14)
; (14)
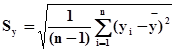 ; (15)
; (15)
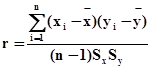 . (16)
. (16)
В (16) r называют коэффициентом корреляции.
Интервал, в котором с установленной (заданной) вероятностью может находиться коэффициент a записывается в виде
A - ta,n-2 SA £ a £ A + ta,n-2 SА  , (17)
, (17)
где A найден по формуле (12), SA – по формуле (13), а ta,n-2 – коэффициент Стьюдента для установленной вероятности и параметра n-2 (n - число измерений).
В серьезных экспериментальных исследованиях вид уравнений измерения обычно неизвестен (не говоря уже об их линейности). В этом случае, сначала из каких-либо соображений выбирают формулу измерения, а затем методом наименьших квадратов вычисляют значения коэффициентов в выбранной формуле.
Рассмотрим конкретный пример применения метода наименьших квадратов для обработки экспериментальных данных.
Пусть для определения коэффициентов a и b проведено 10 пар измерений величин x и y, результаты которых приведены в таблице 1. Если известно, что система уравнений измерения имеет вид (1) и применимы ранее упомянутые ограничения, то воспользуемся формулами, полученными выше.
Вычислим математические ожидания (средние значения) x и y по формулам (9)
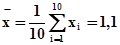
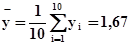 .
.
По формулам (12) и (8) найдем оценки A и B
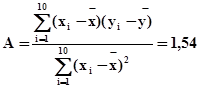 ;
;
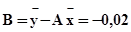 .
.
На рис.2 приведены экспериментальные значения xi и yi и наилучшая прямая, уравнение которой имеет вид
y=1,54x – 0,02 .
Оценка стандартного отклонения для коэффициента A равна
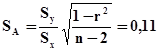 .
.
Интервал, в котором с вероятностью 0,9 может находиться коэффициент a, имеет вид:
a = 1,54 ± 0,21 .
В вычислениях использован коэффициент Стьюдента ta,8 = 1,9 (Таблица 2).
В заключение приведем схему обработки результатов измерений методом наименьших квадратов. Схема применима если уравнения измерений линейны, переменная x не содержит погрешностей, а переменная y распределена нормально и определяется из равноточных измерений (т.е. стандартное отклонение sy одинаково для всех значений yi), причем систематические погрешности пренебрежимо малы.
Результаты измерений записываются в таблицу (см. в качестве примера таблицу 1).
1. Вычисляем коэффициент A
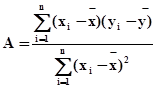 , где
, где 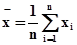 и
и 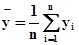 ,
,
n - число измерений.
2. Вычисляем коэффициент B
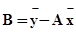 .
.
3. Задаем доверительную вероятность.
4. Вычисляем полуширину доверительного интервала DA
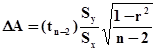 ,
,
где 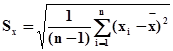 ,
, 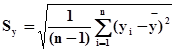 и
и 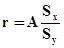 .
.
5. Для коэффициента a записываем выражение a=A ± DA, указав выбранное значение доверительной вероятности.
6. Строим прямую y = Ax + B на графике.
Замечание: Коэффициент Стьюдента tn-2 находится из таблицы 2.
Таблица 2. Коэффициенты Стьюдента tn
| Доверительная вероятность | 0.8 | 0.9 | 0.95 | 0.99 |
| n | ||||
| 3.1 | 6.3 | 12.7 | 63.7 | |
| 1.9 | 2.9 | 4.3 | 9.9 | |
| 1.6 | 2.4 | 3.2 | 5.8 | |
| 1.5 | 2.1 | 2.8 | 4.6 | |
| 1.5 | 2.0 | 2.6 | 4.0 | |
| 1.4 | 1.9 | 2.4 | 3.7 | |
| 1.4 | 1.9 | 2.4 | 3.5 | |
| 1.4 | 1.8 | 2.3 | 3.4 | |
| 1.4 | 1.8 | 2.3 | 3.3 | |
| 1.3 | 1.6 | 2.0 | 2.6 |
Лабораторная работа №2
ОПРЕДЕЛЕНИЕ УВЕЛИЧЕНИЯ МИКРОСКОПА.
ЛИНЕЙНЫХ РАЗМЕРОВ МАЛЫХ ОБЪЕКТОВ С ПОМОЩЬЮ МИКРОСКОПА
Цель работы: научиться пользоваться микроскопом, определять линейные размеры малых объектов.
Приборы: микроскоп, объективный микрометр, срезы капиллярных трубок, стеклянная пластинка.
Введение
Оптическая система микроскопа состоит, в основном, из двух собирающих линз, одна из них обращена к наблюдаемому объекту и называется объективом. Объектив создает действительное обратное изображение А¢В¢ предмета АВ (рис. 1). Размер этого изображения зависит от величины фокусного расстояния объектива и от расстояния между объективом и предметом. Объектив микроскопа имеет маленькое фокусное расстояние, поэтому эту линзу называют короткофокусной. Предмет АВ помещается на расстоянии немного большем фокусного расстояния, в результате изображение А¢В¢ оказывается значительно увеличенным. Это изображение является, в свою очередь, предметом по отношению ко второй линзе (окуляру), которая, действуя, как лупа, дает мнимое, увеличенное изображение А"В" на расстоянии наилучшего видения от глаза наблюдателя. Для нормального глаза это расстояние равно 25см. Буквами О обозначены оптические центры объектива, окуляра и оптической системы глаза.
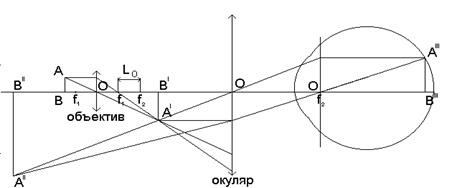
Рис. 1.
Так как лупа дает мнимое изображение, то увеличение лупы определяется как отношение угла, под которым виден (малый) предмет рассматриваемый через лупу, к углу под которым он был виден невооруженным глазом с расстояния наилучшего видения. Можно также сказать, что увеличение лупы есть отношение линейных размеров изображения предмета на сетчатке при рассмотрении его в лупу к линейным размерам изображения того же предмета на сетчатке, когда он рассматривается невооруженным глазом с расстояния наилучшего видения (см. рис. 2).
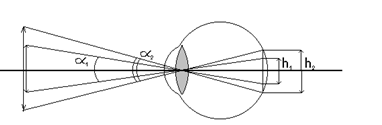
рис. 2.
Из рис. 2 видно, что угол a2, под которым видно изображение, больше угла a1, под которым виден сам предмет, т.е. чем больше угол зрения, тем более крупное изображение получится на сетчатой оболочке глаза. Если угол зрения мал, для его увеличения пользуются оптическими приборами: лупой, микроскопом.
УВЕЛИЧЕНИЕ МИКРОСКОПА
Увеличение микроскопа зависит от увеличения объектива и окуляра. Обозначим увеличение объектива Коб, а окуляра Кок, т.к. линейным увеличением называется отношение длины изображения к длине предмета, тогда
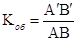
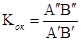 .
.
Перемножив эти равенства почленно, получим
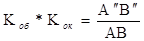 .
.
Отсюда видно, что увеличение микроскопа равно произведению увеличений, даваемых объективом и окуляром в отдельности. Известно, что увеличение лупы (окуляра) равно отношению расстояния наилучшего зрения S к фокусному расстоянию окуляра f2
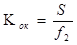 .
.
Увеличение объектива
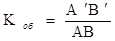 .
.
Из подобия треугольников АВО и А¢ОВ¢ (см рис.1)
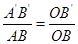 .
.
Принимая BO»f1 (f1-фокусное расстояние объектива). ОВ¢=f1+L0, где L0 - оптическая длина тубуса , т.е. расстояние между задним фокусом объектива и передним фокусами окуляра. Если пренебречь фокусным расстоянием объектива, которое в десятки раз меньше оптической длины тубуса, то ОВ¢»L0. Получим увеличение объектива
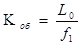 .
.
Тогда увеличение микроскопа
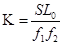 .
.
Итак, увеличение микроскопа зависит от оптической длины тубуса L0, расстояния наилучшего зрения S и фокусных расстояний объектива и окуляра f1, f2.
РАЗРЕШАЮЩАЯ СПОСОБНОСТЬ МИКРОСКОПА
Из формулы, определяющей увеличение микроскопа, можно сделать вывод, что при надлежащем выборе f1 и f2 увеличение микроскопа будет сколь угодно большим. Однако на практике биологи, врачи и другие специалисты, работающие с микроскопами, редко используют увеличения, превышающие 700C - 1500C. Выясним причины такого положения.
Известно, что при попадании света на мелкие объекты, когда размеры объекта соизмеримы с длиной волны, наблюдается явление называемое дифракцией света (более подробно это явление изучается в разделе волновой оптики). За счет этого явления изображением светящейся точки является система концентрических колец, окружающих центральный светлое дифракционное пятно. Поскольку на этот светлое дифракционное пятно приходится основная доля световой энергии (около 84%). Можно пренебречь энергией, приходящейся на остальные дифракционные кольца, и это светлое дифракционное пятно будет являться изображением светящейся точки, которую мы рассматриваем в микроскоп. Угловой размер этого пятна уменьшается с ростом диаметра D объектива микроскопа. При очень малом угловом расстоянии между двумя точками их изображения, получающиеся с помощью какого-либо оптического прибора, накладываются друг на друга и дают одно светящееся пятно. Следовательно, две очень близкие точки не будут восприниматься прибором (глазом) раздельно или, как говорят, не будут разрешаться прибором. Поэтому как бы ни было велико по размерам изображение, на нем не будут видны соответствующие мелкие детали. Обозначим через dY наименьшее угловое расстояние между двумя точками, при котором они еще разрешаются прибором. Величина, обратная dy, называется разрешающей силой оптического прибора.
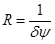 .
.
Угловая полуширина центрального дифракционного максимума определяется выражением
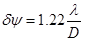 ,
,
где l - это длина волны света, падающего на наблюдаемые объекты, а D - диаметр объектива микроскопа.
Как видно из формулы, один из способов уменьшения угловой полуширины центрального максимума (т.е. радиуса пятна, изображающего наш предмет)- использование света с меньшей длиной волны (ультрафиолетовый микроскоп). При увеличении диаметра объектива разрешающая способность микроскопа повышается. Еще разрешающая способность микроскопа может быть увеличена с помощью специальной жидкой среды с большим показателем преломления (иммерсии) в пространстве между объективом и покровным стеклом микроскопа (иммерсионные микроскопы).
Нужно отметить, что окуляр совершенно не влияет на разрешающую способность микроскопа, он только создает увеличенное изображение объектива.
Из разрешающей способности микроскопа может быть оценено его полезное увеличение, оно то и лежит в пределах от 700 до 1500. При таком увеличении глаз различает все элементы структуры объекта, которые разрешимы объективом.
ПОРЯДОК ВЫПОЛНЕНИЯ РАБОТЫ
1. Определение увеличения объектива.
Для того чтобы определить увеличение объектива, используют объективный микрометр, представляющий собой, нанесенную на стеклянную пластинку, шкалу с делением ценой 0,1мм и окулярный микрометр, заключенный в оправу окуляра. При выполнении работы на предметный столик кладут объективный микрометр, затем перемещая при помощи кримальеры тубус, устанавливают его так, чтобы изображение шкалы объективного микрометра совпало с изображением окулярной шкалы, устанавливают обе шкалы параллельно.
Находят совпадающие на обеих шкалах штрихи делений и отсчитывают количество целых делений шкалы окуляра (nок), совпадающих с целым числом делений изображения объективной шкалы (nоб). Тогда
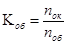
Перемещая на столике объективный микрометр, снова находят совпадающие на обеих шкалах штрихи делений, между которыми укладывается целое число окулярной шкалы. Опыт повторить не менее 3 раз. Результаты наблюдений заносятся в таблицу 1.
Таблица 1
| N опыта | Число делений | Коб | Кок | К | DК | |
| nоб | nок | |||||
| Средние значения |
2. Записать в таблицу 1 увеличение окуляра, обозначенное на окуляре ´8, ´12 и т.д.
3. Найти увеличение микроскопа по формуле К=Коб. × Кок., используя данные таблицы1
4. Определяется среднее значение увеличения микроскопа К и его погрешности DК.
5.Определение размеров малых объектов.
Снимают со столика объективный микрометр и на его место устанавливают исследуемый предмет. Пусть изображение предмета, рассматриваемого в микроскоп, имеет длину, равную n делениям окулярного микрометра. Если бы со шкалой совпал сам предмет, то его длина была бы 0,1 мм×n, так как деление шкалы равно 0,1 мм, но со шкалой совпадает не сам предмет, а его изображение, увеличенное в Коб.. Поэтому истинная длина предмета будет меньше длины изображения. Отсюда
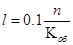 .
.
Размер предмета определяют 5 раз. Результаты заносят в таблицу 2. Определяют среднее значение и погрешность измерения Dl.
Таблица 2.
| N опыта | n | Коб | l, мм | Dl, мм |
| . | ||||
| Средние значения |
ИЗМЕРЕНИЕ ПОКАЗАТЕЛЯ ПРЕЛОМЛЕНИЯ СТЕКЛА
ПРИ ПОМОЩИ МИКРОСКОПА
Пусть из некоторой точки S, находящейся под стеклянной плоскопараллельной пластинкой толщиной d, идет узкий световой пучок расходящихся лучей (рис. 3).
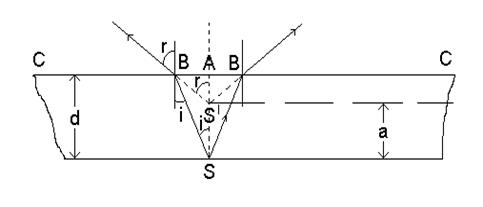
рис. 3
Рассмотрим ход лучей, падающих на поверхность СС под углом i. Закон преломления световых лучей выражен формулой
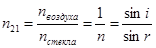 .
.
Или
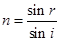 .
.
При переходе света из среды оптически более плотной (стекло) в среду менее плотную (воздух) угол расхождения лучей увеличивается, вследствие чего наблюдателю во второй среде кажется, что лучи исходят из точки S1. Происходит кажущееся приближение точки к наблюдателю.
Из рис. 3 видно, что a = SA –S1A, тогда
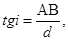
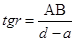 .
.
Учитывая эти соотношения, получим
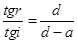
Для малых углов i и r (а только такие лучи от точки S попадают в объектив микроскопа) отношение тангенсов можно заменить отношением синусов, тогда
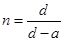
Толщину пластинки d измеряют микрометром. Расстояние a при необходимости и расстояние d-a измеряют при помощи микроскопа, перемещая тубус микрометрическим винтом.
ПОРЯДОК ВЫПОЛНЕНИЯ РАБОТЫ
На предметный столик микроскопа помещают прозрачную стеклянную плоскопараллельную пластинку с черной точкой на ее поверхности. Глядя через окуляр микроскопа и пользуясь микрометрическим винтом, устанавливают тубус микроскопа так, чтобы точка S была отчетливо видна. Записывают в таблицу 3 деления N1 шкалы микрометрического винта, отмечающие данное положение тубуса микроскопа.
Таблица 3.
| N Опыта | Деления шкалы микроскопа | а=N2-N1, мм | Толщина пластинки d,мм | Показатель преломления n | Погрешность измерения Dn | |
| N1,мм | N2,мм | |||||
| Средние значения |
На пластину помещают вторую плоскопараллельную пластину из исследуемого стекла так, чтобы точка оказалась прикрытой ею. Теперь точка выполняет роль источника S (рис. 3). Чтобы снова увидеть точку, нужно поднять тубус микроскопа с помощью микрометрического винта и зафиксировать его положение в момент, когда точка окажется отчетливо различимой (отсчет N2). Разность N2-N1определяет кажущееся поднятие точки (величину а). Вычисляют показатель преломления.
Опыт производят не менее 5 раз, а затем находят среднее значение показателя преломления.
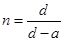
ВОПРОСЫ К РАБОТЕ
1. Постройте изображение предмета в собирающей линзе, если
Дата добавления: 2017-10-04; просмотров: 3744;











