Интерференция света
Интерференцией света называется явление взаимного усиления или ослабления двух когерентных волн при их наложении в пространстве.
Когерентностью называется согласованное протекание во времени и в пространстве нескольких колебательных или волновых процессов. Рассмотрим условия наблюдения интерференции, т.е. попытаемся сформулировать условия когерентности.
Пусть в некоторой точке пространства Р одновременно существуют две произвольные (в общем случае немонохроматические) электромагнитные волны, характеризуемые векторами напряжённостей электрических полей Е1 и Е2.
Френель и Араго обнаружили на опыте, что две световые волны, распространяющиеся в одном направлении, никогда не интерферируют между собой, если Е1 и Е2 перпендикулярны друг к другу, т.е. интерферируют лишь волны, возбуждающие' в некоторой точке пространства колебания одинакового направления.
Е1=Е0соs (w1t +a1) w1t +a1= d1
E2=E0cos (w2t +a2) w2t +a2= d2
 если wl ~w2, то амплитуда результирующего колебания, возникающего в точке Р, находится помощью векторной диаграммы (см. рис .1)и определяется выражением
если wl ~w2, то амплитуда результирующего колебания, возникающего в точке Р, находится помощью векторной диаграммы (см. рис .1)и определяется выражением
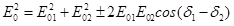 (1)
(1)
Так как средний период колебаний электромагнитного поля в оптической области спектра 10-15с, то ни один приёмник света из-за своей инерционности не позволяет измерить мгновенное значение напряжённости электрического и магнитного поля в световой волне, а также освещённости поверхности. Все приёмники могут измерять только величины, усреднённые за время, не меньше времени разрешения приемника. Усреднённое по времени значение квадрата напряжённости электрического поля называют интенсивностью света, поэтому из (1)
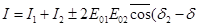 1) (2)
1) (2)
При изменении средней суммарной энергии < 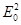 >, мы неизбежно встречаемся с двумя различными результатами опыта в зависимости оттого, что получается при усреднении <
>, мы неизбежно встречаемся с двумя различными результатами опыта в зависимости оттого, что получается при усреднении < 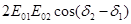 >, называемого интерференционным членом. Результат будет существенно зависеть от разности фаз складывающихся колебаний и изменения этой разности фаз во времени. Если разность фаз d2-d1 беспорядочно и случайным образом меняется во времени, то она может в выделенном конечном интервале времени принимать любые значения от 0 до 2p, поэтому соs принимает значения. ог -1 до +1 и среднее его значение равно 0. В этом случае из уравнения (2) следует, что I=I1+I2.. Если d2-d1=const, то среднее значение cos(d2-d1) равно самому значению cos(d2-d1), поэтому
>, называемого интерференционным членом. Результат будет существенно зависеть от разности фаз складывающихся колебаний и изменения этой разности фаз во времени. Если разность фаз d2-d1 беспорядочно и случайным образом меняется во времени, то она может в выделенном конечном интервале времени принимать любые значения от 0 до 2p, поэтому соs принимает значения. ог -1 до +1 и среднее его значение равно 0. В этом случае из уравнения (2) следует, что I=I1+I2.. Если d2-d1=const, то среднее значение cos(d2-d1) равно самому значению cos(d2-d1), поэтому
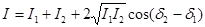 (3)
(3)
Анализируя уравнение (3) сделаем выводы
1) если (d2-d1)=0,2 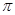 ,4
,4 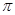 .....2к
.....2к 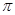 (к=0,1,2,3 и т.д), то cos(d2-d1)=1
(к=0,1,2,3 и т.д), то cos(d2-d1)=1
Е0=Е01+Е02, а 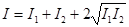 , т.е.
, т.е. 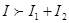
2) если (d2-d1)= p, 3p, 5p .....(2к+1) p , то cos(d2-d1)= -1, Е0=Е01-Е02
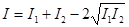 , т.е.
, т.е. 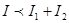
В первом случае происходит усиление результирующего колебания, во втором- ослабление. Если Е01=Е02, то Е0max=2Е01, I=4I1, а Е0min=0, I=0.
Таким образом, усиление или ослабление интенсивности света происходит при определенных условиях, которые можно сформулировать следующим образом:
1) складываемые световые волны должны иметь близкие частоты ( 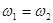 )
)
2) разность фаз d2-d1=const
3) векторы напряженности Е01 и Е02 не должны быть взаимноперпендикулярны.
Колебания или волны, которые удовлетворяют этим условиям называются когерентными.
Так как при cos(d2-d1)=1 наблюдается усиление интенсивности, то условие (d2-d1)= 2к 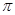 называется условием максиму интенсивности, а условие (d2-d1)= (2к+1)
называется условием максиму интенсивности, а условие (d2-d1)= (2к+1) 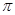 -условие минимума интенсивности.
-условие минимума интенсивности.
Обычно эти условия формулируются не через разность фаз, а через разность хода волн 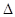 .
.
Пусть S1 и S2 источники света, в точке Р , волны идущие от этих источников накладываются, при этом первая волна проходит путь S1P, а вторая путь S2Р, если волны распространяются в воздухе, то 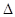 = S2Р- S1P, если волны распространяются в различных средах, то
= S2Р- S1P, если волны распространяются в различных средах, то
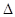 = (S2Р)n2- (S1P)n1, где n1 и n2 показатели преломления соответствующих сред.
= (S2Р)n2- (S1P)n1, где n1 и n2 показатели преломления соответствующих сред.
Разность хода 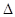 и разность фаз (d2-d1) связаны соотношением
и разность фаз (d2-d1) связаны соотношением
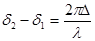
Тогда условия максимума и минимума интерференции могут быть записаны следующим образом:
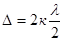 - условие максимума
- условие максимума
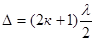 - условие минимума
- условие минимума
ДИФРАКЦИЯ СВЕТА
ПРЕДИСЛОВИЕ
О важности и необходимости изучения явления дифракции студентами – медиками говорит тот факт, что в биомедицинской диагностике достаточно широко используются спектрометры и другие спектральные приборы, составной частью которых является дифракционная решетка. В настоящее время разрабатываются методики, основанные на оптической голографии (см. курс лекций), дающие возможность получения трехмерных изображений исследуемых объектов с хорошей разрешающей способностью и контрастностью. Контуры этих биообъектов могут быть картированны, а их деформации проанализированны в реальном масштабе времени. Эти новые возможности могут оказать влияние на развитие многих разделов медицины: ортопедию, радиологию, офтальмологию, урологию и отологию. В настоящее время в Англии разработана методика диагностики онкологических заболеваний по дифракции рентгеновских лучей на волосе человека. Это совершенно безвредная и безболезненная для человека диагностика, дает возможность распознать заболевание на очень ранних стадиях.
Особенностью лабораторной работы, посвященной проверке соотношения неопределенности Гейзенберга, является взгляд на дифракцию как на проявление чисто квантовых свойств света на макроскопическом уровне. Кроме того, в ней затронуты некоторые философские аспекты квантовой теории, вопросы связанные с понятиями наблюдения и измерения.
Во всех лабораторных работах по дифракции света в качестве источника света используется лазер. В настоящее время лазер достаточно широко используется в медицине, поэтому авторы сочли необходимым включить в это методическое пособие описание принципа работы лазера и привести краткие сведения по его использованию в диагностике, терапии и хирургии.
ДИФРАКЦИЯ СВЕТА
(общие сведения)
Дифракцией света называется явление отклонения света от прямолинейного распространения, когда свет, огибая препятствие, проникает в область геометрической тени.
Качественно поведение света за препятствием может быть объяснено с помощью принципа Гюйгенса, который устанавливает способ построения фронта волны в момент времени t + Dt по известному положению фронта волны в момент времени t. Согласно принципу Гюйгенса каждую точку на первичном волновом фронте следует рассматривать как источник вторичной сферической волны. Поэтому изобразив ряд сферических волн, исходящих из первичного волнового фронта, а затем построив их огибающую, мы получим форму и положение всей волны в более поздний момент времени (рис. 1, среда предполагается неоднородной – скорость волны в нижней части рисунка больше, чем в верхней). На рисунке 2 приведен пример распространения плоской волны через узкую щель.

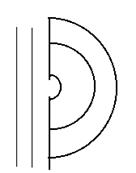
Рис. 1. Рис. 2.
Однако принцип Гюйгенса не дает сведений об амплитуде, а следовательно и об интенсивности волн, распространяющихся в различных направлениях. Френель дополнил принцип Гюйгенса представлением об интерференции вторичных волн. Учет амплитуд и фаз вторичных волн позволяет найти амплитуду результирующей волны в любой точке пространства, Развитый таким способом принцип Гюйгенса получил название принципа Гюйгенса – Френеля. Согласно принципу Гюйгенса-Френеля:
а) каждый элемент волновой поверхности служит источником вторичных сферических волн;
б) амплитуда вторичной волны пропорциональна площади элемента S;
в) амплитуда вторичной волны убывает с расстоянием r от источника по закону 1/r;
г) все вторичные источники являются когерентными.
При вычислении амплитуды колебания, порождаемого световой волной, распространяющейся от реального источника, можно заменить этот источник совокупностью вторичных источников, расположенных непрерывно вдоль волновой поверхности. Определение результирующей амплитуды колебания от всех вторичных источников может быть осуществлено аналитически, методом графического сложения амплитуд или методом зон Френеля.
Различают два случая дифракции света: дифракцию Френеля - дифракцию в сходящихся лучах, и дифракцию Фраунгофера - дифракцию в параллельных лучах. В первом случае на препятствие падает сферическая или плоская волна, а дифракционная картина наблюдается на экране, находящемся позади препятствия на конечном расстоянии от него. Во втором случае на препятствие падает плоская волна, а дифракционная картина наблюдается на экране, который находится в фокальной плоскости собирающей линзы, установленной на пути прошедшего через препятствие света. Дифракцию Фраунгофера можно наблюдать при использовании в качестве источника света лазера, т.к. излучаемые лазером когерентные световые пучки являются коллимированными.
Лабораторная работа№4
ДИФРАКЦИЯ НА НЕКОГЕРЕНТНЫХ ИСТОЧНИКАХ
Целью настоящей работы является изучение дифракции от непрозрачных мелких частиц диаметром несколько микрон (например, эритроцитов), а также измерение их диаметров дифракционным методом. Определение размеров таких меленьких частиц является сложной задачей вследствие невозможности применения обычных средств (микроскопа, проектора, контактных приборов), дающих погрешности, соизмеримые с размерами частиц.
Приборы и принадлежности: лазер, оптическая скамья, дифракционная решетка, стекла с мазками крови, экран со шкалой.
Дифракция Френеля от круглого диска
Рассмотрим сферическую волну, распространяющуюся в изотропной однородной среде от точечного источника S. Поместим между источником S и точкой наблюдения P непрозрачный круглый диск радиуса r (рис. 3).
Согласно принципу Гюйгенса-Френеля каждая точка волновой поверхности является источником элементарных вторичных волн, распространяющихся во всех направлениях, причем эти вторичные волны интерферируют между собой. Рассмотрим волны, идущие от открытой части волновой поверхности, собирающиеся в точке Р экрана. Они являются когерентными и интерферируют. Интенсивность света в точке наблюдения Р, как результат интерференции, можно легко определить с помощью метода зон Френеля, который заключается в следующем.
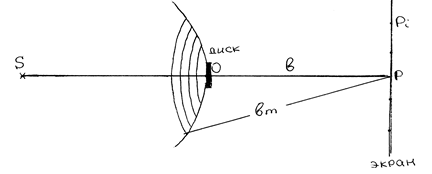
Рис. 3.
Фронт распространяющийся волны разбивается на области, называемые зонами, так чтобы разность хода вторичных волн от соответствующих точек двух соседних зон до рассматриваемой точки Р были равны половине длины волны. Таким образом, в точку наблюдения волны от соседних зон приходят с противоположными фазами и при наложении они будут ослаблять друг друга. Задача расчета интерференции вторичных волн фактически сводится к определению количества зон Френеля. В соответствии с определением зоны Френеля следует, что расстояния bm от внешнего края m-ой зоны до точки P равно
bm = b + m×l/2 ,
где b - расстояние от вершины волновой поверхности O до точки P, m - целое число, соответствующее номеру зоны Френеля.
Волны, приходящие в точку P из двух соседних зон, находятся в противофазе, т.е. их разность фаз в точке наблюдения равна p.. Площади зон Френеля примерно одинаковы. Расстояние bm от зоны до точки P медленно растет с ростом номера зоны m, поэтому ( вторичная волна - сферическая) амплитуда Am колебания, возбуждаемого m-ой зоной в точке P, монотонно убывает.
A1 > A2 > A 3 > …….. > Am-1 > Am > Am+1 >….
Т. к. фазы колебаний, возбуждаемые соседними зонами, отличаются на p, то амплитуда результирующего колебания в точке Р может быть представлена
A = A1 - A2 + A3 – A4 +………..
Если диск закроет m первых зон Френеля, амплитуда в точке P будет равна
A = Am+1 – Am+2 +Am+3 – Am+4 + ….
Запишем это выражение в следующем виде:
A = Am+1 / 2 + ( Am+1 / 2 – Am+2 + Am+3 / 2) +….
Вследствие монотонного убывания Am , приближенно можно считать, что
Am+1 / 2 + Am+3 / 2 = Am+2 ,
тогда все выражения в скобках равны 0, следовательно
A = Am+1 / 2 .
Эта формула дает результирующую амплитуду волн, достигших экрана в точке Р. Так как интенсивность I пропорциональна амплитуде в квадрате A2, то получается результат парадоксальный с точки зрения геометрической оптики. За непрозрачным диском, на его оси всегда будет светлое пятно. Его называют пятном Пуассона. Это светлое пятно имеет вид круглого пятнышка, если рассматривалась дифракция на круглом диске и прямой полоски, если рассматривалась дифракция на прямоугольной пластинке. Это значит, что световые волны огибают круглый диск по всему его краю и вследствие симметрии встречаются на оси диска. Это дает возможность получить изображение какого-либо предмета без оптической линзы с помощью круга или шара.
Рассмотрим результат действия открытой волновой поверхности для точки Pi, смещенной относительно точки Р в любом радиальном направлении, диск будет перекрывать часть (m + 1)-й зоны Френеля, одновременно откроется часть m-ой зоны. Это вызовет уменьшение интенсивности. При некотором

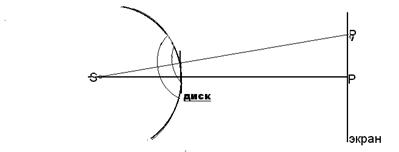
Рис. 3,а.
положении точки Рi интенсивность достигнет минимума. Если сместиться из центра еще дальше, диск перекроет дополнительно часть ( m + 2)-oй зоны, одновременно откроется часть (m - 1)-oй зоны. В результате интенсивность возрастет и в точке P достигнет максимума.
Дифракционная картина, которая будет наблюдаться на экране, помещенном за диском, может быть изображена зависимостью интенсивности света I от расстояния R (рис. 4), отсчитанного от точки Р до точки Pi (рис. 3,а). Если обозначим интенсивность центрального максимума I0, то интенсивность последующих максимумов определяется следующими соотношениями I1 = 0,045I0; I2 = 0,016I0; I2 = 0,008I0 и т.д.
Таким образом, центральный максимум значительно превосходит по интенсивности остальные максимумы; в нем сосредотачивается основная доля светового потока открытой волновой поверхности.
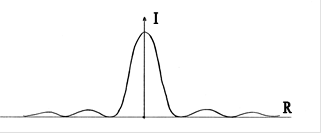
Рис. 4.
Можно найти и аналитическое выражение зависимости IPi от R. Это достаточно сложное выражение, анализ которого дает возможность найти условия минимума и максимума для данной дифракционной картины. В случае непрозрачного круглого диска дифракционная картина имеет вид чередующихся светлых и темных концентрических колец. Если круглый диск имеет радиус r , то положение минимумов интенсивности определяется следующими выражениями:
r sin a1 = 0,61l ; r sin a3 = 1,11 l ; r sin a5 = 1,62 l (1)
Максимумов -
r sin a2 = 0,81 l ; r sin a4 = 1,33 l ; r sina6 = 1,86 l (2).
Углы ai - это углы наблюдения соответствующих минимумов и максимумов. Роль круглого диска могут выполнить эритроциты крови. Но один-единственный диск столь малого размера (6 - 8 мкм) даст крайне слабую дифракционную картину. Картина будет проектироваться на светлый фон, создаваемый прямым недифрагированным пучком света. Только тысячи таких частичек способны дать картину, хорошо видимую глазом. Если взять мазок крови, то мы получим слой беспорядочно расположенных непрозрачных дисков. При одновременном присутствии в сечении светового пучка многих частиц, угловое распределение дифрагированного света, создаваемого каждой частицей в отдельности, не нарушается, если нет интерференционного эффекта между световыми пучками, дифрагировавшими на разных частицах. Если в плоскости поперечного сечения светового пучка частицы расположены хаотично, то разность фаз между дифрагированными пучками от разных частиц будет меняться также хаотично и интерференция будет отсутствовать. Тогда интенсивность дифрагированного в данном направлении света равна сумме интенсивностей световых пучков, дифрагированных на разных частицах. Поэтому дифракционная картина, создаваемая одним эритроцитом будет усилена в N раз ( N - число частиц).
Наблюдая дифракционную картину от N эритроцитов на экране и используя соотношения (1) и (2), можно определить размеры частиц, на которых наблюдалась дифракция.
Определение размеров мелких частиц
Для определения размеров мелких частиц составим следующую схему эксперимента - рис. 5.



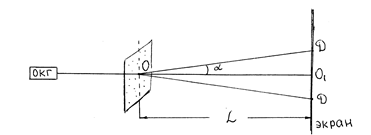
Рис. 5.
На рисунке цифрами обозначены: 1 - Лазер непрерывного излучения; 2 - Стеклянная пластинка с мазком крови, которую вставляют в рейтер, легко перемещающийся вдоль оптической схемы; 3 - Непрозрачный экран с миллиметровой шкалой.
ИЗМЕРЕНИЯ
1. Включить лазер с помощью тумблера «Сеть» на панели блока питания лазера.
2. Установить экран так, чтобы пучок света лазера был направлен точно в центр экрана.
3. На расстоянии примерно 0.5 м от экрана установить рейтер со стеклянной пластинкой. На экране должна быть видна дифракционная картина, представляющая собой яркое пятно, окруженное концентрическими темными и светлыми окружностями. Дифракционная картина должна быть симметрична относительно перекрестия шкалы экрана.
4. Измерить диаметры темных и светлых дифракционных колец D . Измерения производятся по серединам колец.
5. Измерить расстояние L от плоскости стеклянной пластинки с мазком крови до экрана по шкале оптической скамьи.
6. Результаты измерения занести в таблицу 1.
7. Поскольку диаметры дифракционных колец, наблюдаемых на экране много меньше расстояния L, можно считать что
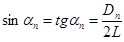 (3)
(3)
и, используя условия минимумов и максимумов получим соотношения для нахождения радиуса эритроцитов
D1 / 2L = 0.61 l / r ; D2 / 2L = 0.82 l / r ; D3 = 1.11 l / r (4) D1, D3, D5,…- диаметры темных дифракционных колец;
D0, D2, D4, D6,…- диаметры светлых дифракционных колец.
Длина волны излучения лазера l = 633 нм. Найдем по формулам (4) радиус эритроцитов, а затем средний радиус.
| Номер кольца | интенсивность | D | L | Радиус частиц (м) | rср. (м) |
| 0. | Cветлое | ||||
| 1. | Темное | ||||
| 2. | Светлое | ||||
| 3. | Темное | ||||
| 4. | Светлое | ||||
| 5. | Темное |
8. Переместить пластинку с мазком крови вдоль оптической скамьи.
9. Повторить пункты 4-7 при трех положениях пластинки с мазком крови относительно экрана.
10. Сравнить полученные результаты и сделать вывод зависит ли диаметр дифракционных колец от размеров частиц, от расстояния от частиц до экрана.
11. Оценить погрешность измерения радиусов эритроцитов для любого опыта.
12. Записать конечный ответ в форме 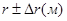 при a =
при a =
13. Найти относительную погрешность.
Контрольные вопросы
1. В чем заключается явление дифракции света?
2. Как зависит характер дифракционной картины от числа частиц, падающих в пучок лучей?
3. С помощью метода зон Френеля оцените результат действия неограниченной сферической волны на экране в точке Р.
4. Почему размеры очень маленьких частиц порядка нескольких (мк) нельзя измерять микроскопом?
5. Изобразите зоны Френеля на плоском фронте волны.
6. Можно ли изменяя расстояние L, получить в центре дифракционной картины темное пятно?
Лабораторная работа№5
ДИФРАКЦИЯ НА ОДНОЙ ЩЕЛИ И СИСТЕМЕ С БОЛЬШИМ
ЧИСЛОМ ЩЕЛЕЙ – ДИФРАКЦИОННОЙ РЕШЕТКЕ
Цель работы: научиться по дифракционной картине определять длину волны когерентного излучения и измерять размеры малых объектов.
Приборы и принадлежности: лазер, оптическая скамья, дифракционная решетка, прямоугольная щель, экран, линейка.
ДИФРАКЦИЯ ФРАУНГОФЕРА НА ЩЕЛИ
Пусть на очень длинную прямоугольную щель ширины b падает по нормали к ней плоская световая волна. Если экран расположен бесконечно далеко от щели или за щелью находится линза, направляющая на экран пучки параллельных лучей, то наблюдается дифракция Фраунгофера. Поместим за щелью собирающую линзу, а в фокальной плоскости линзы экран (рис. 1):

Рис. 1.
Волновые поверхности падающей волны, плоскость щели и экран параллельны друг другу. Согласно принципу Гюйгенса-Френеля элементарные участки открытой части волновой поверхности являются источниками вторичных волн, распространяющихся в разных направлениях.
Лучи, образующие угол q с нормалью к плоскости щели, собираются в точке P экрана. Они являются когерентными и интерферируют. Результат интерференции легко определить с помощью метода зон Френеля, который заключается в следующем.
Разобьем открытую часть волновой поверхности на зоны параллельные краям щели так, чтобы разность хода лучей от краев соседних зон до точки наблюдения была равна половине длины световой волны l / 2. Такие зоны называются зонами Френеля.
Колебания, приходящие в точку наблюдения от каждой пары соседних зон взаимно погашают друг друга, так как находятся в противофазе. Разность хода от краев щели D = b sinq. Если для точки наблюдения Р разность хода равна четному числу l / 2, т.е. в щели укладывается четное число зон Френеля, амплитуда колебаний в этой точке равна нулю. Таким образом, условием минимума интерференции является равенство разности хода лучей от краев щели четному числу полуволн или целому числу длин волн
b sinq = ± ml ; (m = 1, 2, 3, ...) . (1)
Если для точки Р разность хода равна нечетному числу полуволн, число зон Френеля будет нечетным, действие одной из них окажется неcкомпенсированным и наблюдается максимум интенсивности.
В случае q = 0 все колебания оказываются в фазе, поэтому в центре экрана наблюдается светлая полоса, соответствующая максимуму нулевого порядка. Интенсивность этого максимума наибольшая. При
sin q = ± l / b, ± 2l / b, ± 4l / b
наблюдаются минимумы соответственно 1-го, 2-го и. т.д. порядков. При
sin q = ± 3l / b, ±5l / b, ±7l / b
наблюдаются максимумы 1-го, 2-го и т.д. порядков. График зависимости интенсивности от угла дифракции изображен на рис. 2.
 Sin q
Sin q
Рис. 2.
ДИФРАКЦИОННАЯ РЕШЕТКА
Дифракционной решеткой называется совокупность большого числа N отстоящих друг от друга на одно и то же расстояние щелей. Расстояние между серединами соседних щелей d называется периодом решетки (рис. 3). Выясним характер дифракционной картины, получающейся на экране при падении на решетку параллельных световых волн.
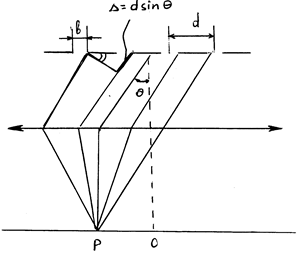
Рис. 3.
Каждая из щелей даст на экране картину, описываемую графиком приведенным на рис. 2. Картины от всех щелей придутся на одно и то же место экрана. Если бы колебания, приходящие в точку P от различных щелей были некогерентными, результирующая картина от N щелей отличалась бы от картины, создаваемой одной щелью, лишь тем, что все интенсивности возросли бы в N раз. Однако, колебания от различных щелей будут интерферировать между собой, Поэтому дифракционная картина от дифракционной решетки будет иной, чем от одной щели.
Проанализируем распределение интенсивности в этой картине. Для нахождения интенсивности в каждой точке экрана мы должны найти результирующую амплитуду колебаний в этой точке. Арез = å Аi , (2)
где Ai - результирующая амплитуда от каждой отдельной щели.
Для направлений, удовлетворяющих условию минимума для каждой отдельной щели (1), все Ai равны 0, поэтому и амплитуда результирующего колебания в соответствующей точке экрана будет равна нулю. Таким образом, условие минимума (1) для одной щели является также условием минимума для решетки
b sin q = ± ml .
Это условие так называемых главных минимумов. Из рис. 3 видно, что разность хода лучей от соседних щелей равна D = d sin q. Если D равно целому числу длин воли, колебания от отдельных щелей приходят в фазе и суммарная амплитуда колебаний в соответствующей точке экрана равна Амакс. = N Аi. Поэтому условием главных максимумов является
d sin q = ± ml . (3)
Число m дает порядок главного максимума. В центре экрана образуется самый интенсивный максимум нулевого порядка, по обе стороны от него располагаются максимумы, первого, второго и т.д. порядков. В направлениях, определяемых формулой (3), при отдельных значениях m могут и не возникать максимумы. Это будет в направлениях, для которых каждая отдельная щель решетки имеет минимум. Допустим d = 2b , тогда условие появления главного максимума m = 2 имеет вид d sin q = 2l или b sin q = l, т.е. переходит в условие минимума (1). Отсюда следует, что в этом случае все главные максимумы четных порядков не появятся.
Кроме главных минимумов, определяемых условием (1), в промежутках между соседними главными максимумами имеется по (N-1)-му добавочному минимуму. Эти минимумы возникают в тех направлениях, для которых колебания от отдельных щелей погашают друг друга.
Условие добавочных минимумов легко получить методом графического сложения колебаний. Колебания от отдельных щелей изображаются векторами одинаковой длины. Каждый из последующих векторов повернут относительно предыдущего на один и тот же угол d равный разности фаз колебаний, приходящих от соседних щелей. Если ломаная линия, составленная из этих векторов, замкнутая (рис. 4), то амплитуда колебаний, возбуждаемых всей решеткой в соответствующей точке равна нулю, т.е. получается дифракционный минимум.
. 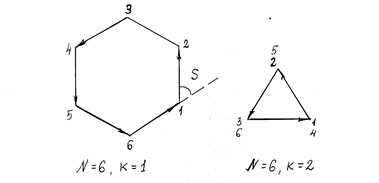
Рис. 4.
Произведение d на число щелей N в этом случае кратно 2p
dN = 2pk или d = 2pk / N .
Учитывая, что
d = 2pD / l = 2pd sinq / l ,
получаем условие добавочных минимумов
d sin q = ± kl / N , (4)
где k = 1,2,……N-1, N+1, …..2N-1,2N+1,… принимает все целочисленные значения кроме 0, N, 2N, ..., при которых условие (4) переходит в (3).
Между добавочными минимумами располагаются слабые дополнительные максимумы. Распределение интенсивности в дифракционной картине от решетки для N = 6 и d / b = 3 приведено на рис. 5. Штриховой линией показана интенсивность I(q) от одной щели, умноженной на N2.
 Sin q
Sin q
Рис. 5.
ПОРЯДОК ВЫПОЛНЕНИЯ РАБОТЫ
1. Используя условие главных максимумов (3), определить длину волны лазера
l = d sinq / m .
Для этого в соответствии со схемой эксперимента (рис. 6), поставить дифракционную решетку на пути лазерного луча, так чтобы на экране были отчетливо видны дифракционные максимумы 1-го и 2-го порядков.
2. Измерить расстояние L от решетки до максимума m-го порядка.
3. Определить Xm - расстояние от центра экрана до максимума m-го порядка как половину расстояния между симметрично расположенными максимумами (для большей точности).
4. Рассчитать длину волны лазера по формуле
l = d Xm / mL (5)
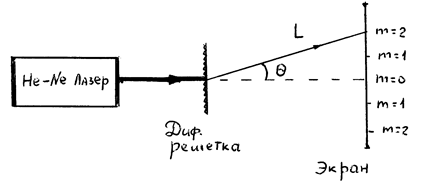
Рис. 6.
Примечание: Постоянная решетки d указана на дифракционной решетке.
5. Данные измерений и расчетов записать в таблицу 1.
Таблица 1.
| N | d, мм | L, см | M | 2Xm, см | Xm ,см | l, нм | lcp, нм | l ± Dl |
| 1 2 3 |
6. Оценить погрешность измерения l и округлить результат в соответствии с погрешностью.
Определение ширины узкой щели.
1. На пути луча лазера поместить узкую щели и получить на экране картину чередующихся дифракционных минимумов и максимумов.
2. измерить расстояние между щелью и минимумом m-го порядка.
3. Измерить расстояние 2Хm между симметрично расположенными минимумами 1-го, 2-го и т.д. порядков.
4. Записать в таблицу 2 данные измерений и значение l, полученное в опыте 1.
5. Рассчитать ширину щели b по формуле (6). Из формулы (1)
b = ml / sinq или b = mlL / Xm
6. Оценить погрешность измерения b.
Таблица 2.
| N | l, нм | L, см | m | 2Xm, см | X m, см | b, мм | bcp, мм | b ± Db |
КОНТРОЛЬНЫЕ ВОПРОСЫ И ЗАДАНИЯ
1. В чем заключается явление дифракции?
2. Выведите условие минимума при дифракции на щели методом зон Френеля.
3. Что наблюдается на экране при ширине щели b < l ? Почему?
4. Нарисуйте график зависимости интенсивности от sinq при дифракции на щели.
5. Объясните условия возникновения главных максимумов и минимумов при дифракции на решетке.
6. Объясните с помощью векторной диаграммы условие дополнительных минимумов при дифракции на решетке.
7. Нарисуйте примерный график зависимости интенсивности от sinq для дифракционной решетки с N = 4 и d / b = 2.
8. Как определяется в работе длина волны лазерного излучения?
9. Как определяется ширина щели?
10. Почему максимумы дифракционной картины от решетки более яркие и узкие, чем щели?
Лабораторная работа №6
РАСПРЕДЕЛЕНИЕ ИНТЕНСИВНОСТИ В ДИФРАКЦИОННОЙ
КАРТИНЕ ОТ ОДНОЙ ЩЕЛИ
Цель работы: изучение распределения интенсивности в картине дифракции от узкой щели при наблюдении в свете лазера.
Приборы и принадлежности: лазер, узкая щель с параллельными краями, экран, оптическая скамья с линейкой, фоторегистратор - фотодиод с электронным усилителем и микроамперметром.
ВВЕДЕНИЕ
Изучение распределения интенсивности в дифракционной картине от одной щели рассмотрим на примере дифракции Фраунгофера. Схема наблюдения дифракции Фраунгофера представлена на рис. 1. Параллельный пучок от Не — Ne- лазера 1 падает нормально на щель 2, длина которой много больше ее ширины b. Согласно принципу Гюйгенса-Френеля, каждая точка плоскости щели, до которой дошло световое колебание, становится источником вторичных сферических волн. Вторичные волны являются когерентными и интерферируют при наложении. Результат интерференции в виде периодического распределения интенсивности наблюдается на экране 3, находящемся на расстоянии l > b2/l от щели 2.
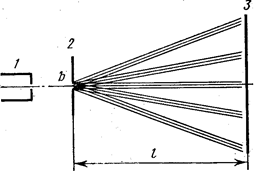
Рис. 1.
Распределение интенсивности в получаемой картине определяется суммированием вторичных волн, пришедших в данную точку экрана от всех элементов щели, с учетом их амплитуды и фазы по принципу Гюйгенса - Френеля.
При небольших углах дифракции наиболее просто рассчитать интенсивность света на экране графическим методом, предложенным Френелем. Для этого разобьем открытую часть волнового фронта в плоскости щели на равные по площади узкие полоски (подзоны), аналогичные зонам Френеля, но гораздо меньше по ширине, полоски параллельны краям щели. В данном случае фронт волны – плоскость, т.к. используется коллимированный пучок. Каждая полоска (подзона) будет играть роль элементарного вторичного источника волн. Волна от каждой полоски (подзоны) имеет одинаковую амплитуду DА, а разность фаз от соседних полосок (подзон) обозначим d, она зависит от угла дифракции j (см. рис. 2), определяющего направление на точку наблюдения Р.
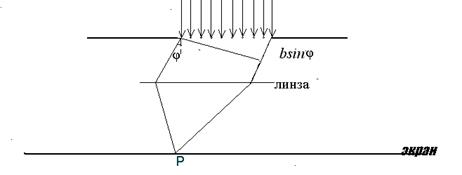
Рис. 2.
Колебание, создаваемое в точке Р каждой такой полоской, можно представить в виде вектора, длина которого равна амплитуде колебания DА, а угол, образуемый вектором с направлением, принятым за начало отсчета, дает начальную фазу колебания. Результирующая амплитуда колебания, создаваемого в точке Р совокупностью всех полосок (подзон), определится векторной диаграммой, получающейся при векторном сложении колебаний, возбуждаемых отдельными подзонами. При j = 0 разность фаз d равна нулю и векторная диаграмма имеет вид, показанный на рис. 3,а. Амплитуда результирующего колебания А0 равна алгебраической сумме амплитуд складываемых колебаний.
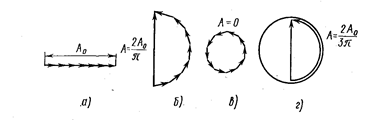
Рис. 3.
Если разность фаз складываемых колебаний, соответствующих краям щели, равна p (т. е. разность хода D = b sin j = l/2), то векторы DА располагаются вдоль полуокружности длиной А0 (рис. 3,б). Следовательно, для результирующей амплитуды получим значение А = 2А0/p. В случае, когда D = b sin j = l, колебания от краев щели отличаются по фазе на 2p. Соответствующая векторная диаграмма дана на рис. 3, в. Векторы DА располагаются вдоль окружности длиной А0. Результирующая амплитуда равна нулю, что соответствует первому минимуму. Второй максимум наблюдается при D = bsinj = 3l/2. В этом случае колебания от краев щели отличаются по фазе на Зp. Строя последовательно векторы DА, мы обойдем полтора раза окружность диаметра А1 = 2А0/(Зp) (рис. 3,г) и т.д. Таким образом, амплитуда A1 первого максимума составляет 2/(p) от амплитуды А0 нулевого максимума, а интенсивность I1 = A  = [2/(p)]A
= [2/(p)]A  » 0,045 I0. Аналогично можно найти и относительную интенсивность остальных максимумов. В результате получаются следующие соотношения интенсивностей:
» 0,045 I0. Аналогично можно найти и относительную интенсивность остальных максимумов. В результате получаются следующие соотношения интенсивностей:
I0:I1:I2:I3:……:In=1:(2/p)2:(2/3p)2:(2/5p)2:…=1:0,045:0,016:0,008 . (1)
Таким образом, центральный (нулевой) максимум значительно превосходит по интенсивности остальные максимумы. Ему соответствуют ~ 90 % всего светового потока, выходящего из щели. Строя векторные диаграммы для различных значений угла дифракции j, можно заметить, что максимумы (т.е. результирующая амплитуда не равна нулю) получаются при условии
D=bsinjk= (2k+1) l/2 . (2)
Результирующая амплитуда равна нулю при углах дифракции, определяемых условием
bsinjk= ± kl . (3)
Следовательно, (2) будет условием дифракционного минимума, а k = 1,2,3,... - порядок дифракционного минимума. При k = 0, как видно j0 = 0 и условие bsinj0 = 0 будет условием максимума нулевого порядка.
Положение минимумов интенсивности определяется выражением
sinjk = kl/b , ( 4)
которое следует из (3). Так как модуль sinjk не может превысить 1, то kl/b £ 1, отсюда k £ b/l -этим соотношением определяется количество минимумов интенсивности, которое может наблюдаться на щели данной ширины b.
График распределения интенсивности на экране 3 показан на рис. 4. Вид дифракционной картины Фраунгофера зависит от ширины щели. Если, например, ширина щели b = l, то sinj1 = 1, а следовательно, и j1= p/2, таким образом центральный максимум расплывается на всю плоскость экрана. При b >> l угол ди-
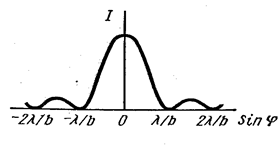
Рис. 4.
фракции, соответствующий первому минимуму, значительно меньше p/2 и картина может оказаться слишком мелкой для наблюдения.
В настоящей работе предлагается составить схему дифракции от щели, позволяющую отчетливо наблюдать дифракционную картину и построить экспериментальный график распределения интенсивности.
ОПИСАНИЕ УСТАНОВКИ
Установка собирается по схеме рис. 5.

Рис. 5.
Лазер 1 устанавливается на оптической скамье так, чтобы часть скамьи (не менее 1 м) оставалась свободной. На свободном конце скамьи устанавливаются два рейтера: один с державкой для щели 2, другой со сменной державкой для матового экрана 3, а также для фотодиода 4. Державка для щели должна иметь устройство для небольшого перемещения в поперечном направлении при наладке установки. Державка для фотодиода должна быть снабжена поперечными направляющими для перемещения фото
Дата добавления: 2017-10-04; просмотров: 1730;











