Структура системы управления беспилотным летательным аппаратом.

Схема системы управления угловой ориентацией БПЛА с элементами оптимальной оценки регулирования приведена на рис.6.1

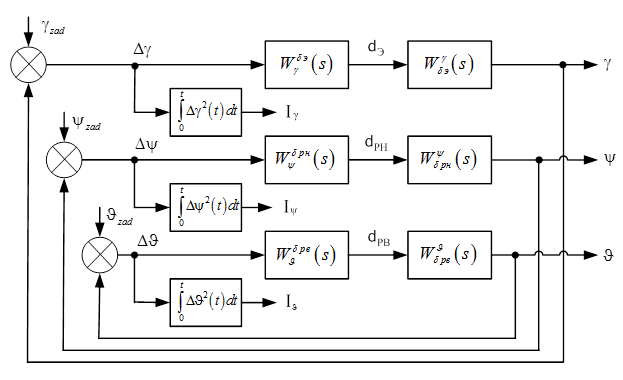
Рис. 6.1. Структурная схема системы управления БПЛА

с элементами оптимальной оценки

Управляемые углы крена 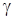, рысканья 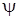и тангажа 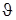вычитаются из заданных углов крена 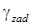, рысканья 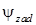и тангажа 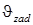. Операция вычитания обусловлена тем, что передаточные функции БПЛА инвертируют знак

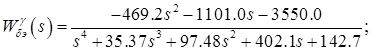
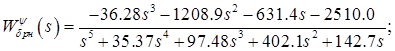
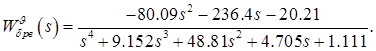
Рассогласования углов поступают в автопилот, включающий в себя три канала управления: канал управления креном 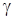, воздействием на элероны 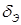, канал управления углом рысканья 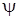, воздействием на руль направления 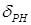, и канал управления углом тангажа 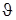, воздействием на руль высоты 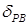. Передаточные функции каналов автопилота синтезированы в лаб. раб. 5 и описываются передаточными функциями

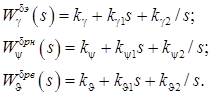
Параметры автопилота вычислены из условия получения заданного качества и не являются оптимальными. Под оптимальностью понимается получение наилучших показателей в соответствии с выбранным критерием качества. Наибольшее распространение получил квадратичный интегральный критерий качества. Используем именно этот критерий для нахождения оптимальных коэффициентов автопилота.

В соответствии с квадратичным интегральным критерием качества наиболее высокое качество имеет система с минимальной площадью под кривой переходной характеристики, текущие значения которой возведены в квадрат. Критерий применим для характеристик как с положительными значениями, так и для знакопеременных. Вычисленное значение интеграла всегда будет положительным, его величина будет минимальной при минимальных интегральных показателях: отклонению от установившегося значения и длительности.

Выполним оптимизацию заданного канала автопилота по двум параметрам: коэффициенту усиления при производной и коэффициенту усиления при интеграле. Коэффициент усиления пропорциональной части определим исходя из заданной статической или скоростной погрешности регулирования.

Интегрирование переходной характеристики по рассогласованию исключает большую составляющую установившегося значения. В иных случаях из текущих значений переходной характеристики необходимо вычитать установившееся значение. В связи с тем, что выполняется оптимизация следящей системы с выходным сигналом по рассогласованию, квадратичные интегральные оценки качества (интеграл качества) для каналов автопилота запишем в виде

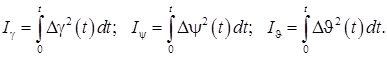
В процессе оптимизации необходимо подобрать такие параметры автопилота, при которых соответствующий интеграл имеет минимальное значение. Выполнение такого поиска требует использования методов планирования эксперимента.

6.3.2. Выбор и построение плана поиска оптимальных параметров автопилота.

Поиск оптимальных параметров автопилота можно выполнить перебором возможных сочетаний искомых коэффициентов в достаточно широком диапазоне. Однако такое решение неэкономично т. к. связано с большими экспериментальными затратами. Несколько экономичней стратегия грубого поиска, когда возможное положение экстремума определяется перебором сочетаний искомых коэффициентов с большим шагом. Затем в области предполагаемого экстремума выполняется поиск с меньшим шагом и т. д. до тех пор пока величина шага станет меньше допустимой погрешности определения оптимальных параметров. Если точность определения оптимальных параметров достаточно высока, то число опытов даже в ограниченном диапазоне окажется чрезвычайно большим.

Известны более экономичные планы эксперимента, отвечающие требованиям минимизации объёма экспериментальных исследований и высокой точности определения оптимальных параметров. К таким планам относят, например, метод крутого восхождения или градиентный метод. Суть метода заключается в том, что при некотором произвольно выбранном сочетании искомых параметров в области возможного их изменения, вычисляется градиент искомой функции 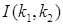, где – интеграл качества; 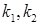– искомые коэффициенты автопилота. Поиск максимума выполняется по направлению градиента. Для поиска минимума интеграла качества необходимо выбрать обратное направление. Далее строится однофакторный план эксперимента. Можно использовать простой перебор сочетаний искомых параметров в выбранном направлении или использовать поиск методом «золотого сечения».

Для поиска оптимальных параметров автопилота в данной работе выберем более распространённый метод – последовательный симплексный метод. Метод не требует сложных промежуточных вычислений, поддаётся автоматизации и применяется даже в тех случаях, когда направление поиска описывается нелинейной зависимостью от искомых параметров.

В основе метода лежит симплекс – это фигура с минимальным числом вершин в пространстве, не принадлежащих пространству меньшей размерности. В данном эксперименте искомые коэффициенты автопилота назовём факторами, а интеграл качества назовём откликом. Таким образом, результатом реализации плана эксперимента является нахождение таких значений факторов, при которых отклик имеет минимальное значение. Так как в эксперименте участвуют два фактора, назовём план эксперимента двухфакторным. План можно построить на плоскости, симплекс представим равносторонним треугольником. Вершины симплекса представим элементами массива 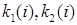, где i – номер вершины симплекса, i – м факторам соответствует 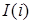отклик. Положение первой точки симплекса зададим с факторами, полученными в лаб. раб. 5. Положение второй и третьей точек выберем из соотношений (рис. 5.2)

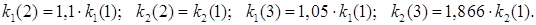
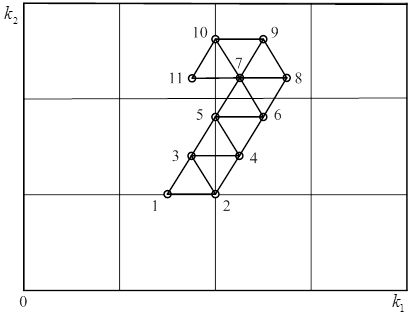
Рис.5.2. Графическое представление поиска оптимальной точки

симплексным методом

Выполняются вычисления отклика в трёх точках первого (начального) симплекса. Анализируются полученные результаты. В зависимости от величины отклика в вершинах симплекса выбирается худшая вершина. При движении к минимуму худшей вершиной является вершина с наибольшей величиной отклика. Пусть ею будет точка 1. Переворачиваем (отражаем) симплекс через грань, противолежащую худшей точке 1, т. е. через грань с вершинами 2 и 3. Координаты вершины отражённого симплекса (точку 4) вычисляем в соответствии с выражениями

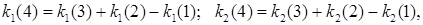
где 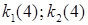– координаты новой вершины в отражённом симплексе; 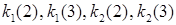– координаты сохранённых вершин в новом симплексе; 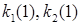– координаты отражённой вершины.

Выполняется вычисление отклика в четвёртой точке отражённого симплекса. Анализируются полученные результаты. Отражается симплекс через грань, противолежащую худшей точке. Вычисляются координата новой точки симплекса, выполняется измерение отклика в новой точке и т. д.

Эксперимент и расчёты продолжаются до тех пор, пока не произойдёт зацикливания симплексов вокруг одной точки. На рис. 5.2 этой точкой является точка 7. Координаты этой точки будем считать оптимальными параметрами канала автопилота.

Если точность определения оптимальных параметров недостаточна, то можно уменьшить размер грани симплекса и продолжить эксперимент до получения требуемого результата.