И силовая функция МТ
Среди сил, действующих на МТ, встречаются силы, зависящие только от положения этой МТ и времени.
Определение: Силовым полем называют часть пространства, в каждой точке которого на МТ действует определенная сила, зависящая от координат МТ и времени.
Определение:Силовое поле считается стационарным, если действующие силы не зависят от времени. Если же силы зависят от времени, то силовое поле называется нестационарным.
Предположим, что существует такая функция координат и времени U(х, у, z, t), частные производные которой по координатам равны проекции силы силового поля на соответствующие координатные оси, т. е.
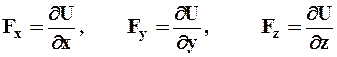 . (4.46)
. (4.46)
Определение:Функция U(х, у, z, t) называется силовой функцией данного силового поля, а само силовое поле называется потенциальным или консервативным, сила же потенциального силового поля называется потенциальной или консервативной.
Примерами консервативных сил являются сила тяжести, сила упругости и сила всемирного тяготения.
При наличии силовой функции выражение для элементарной работы силы потенциального стационарного силового поля примет вид:
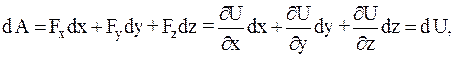
т.е.
dA = dU. (4.47)
Таким образом, элементарная работа силы в потенциальном стационарном силовом поле равна полному дифференциалу силовой функции.
Полная работа силы 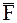 на участке от точки В0 до точки В можно выразить следующим образом:
на участке от точки В0 до точки В можно выразить следующим образом:
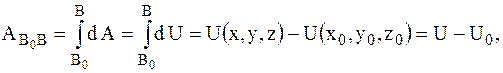 т. е.
т. е.
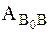 = U – U0, (4.48)
= U – U0, (4.48)
где 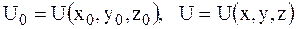 .
.
Следовательно, полная работа силы на каком-либо перемещении МТ равна разности значений силовой функции в конечной и начальной точках перемещения и не зависит от формы траектории, по которой оно совершается, если силовая функция является однозначной.
Из (4.48) следует, что работа силы в потенциальном стационарном силовом поле по любому замкнутому пути равна нулю, если значение силовой функции в начальной и конечной точках перемещения одинаково, т. е. силовая функция является однозначной.
Дата добавления: 2016-06-05; просмотров: 1637;











