Работа произвольной системы сил, приложенной к СМТ
Пусть к свободной СМТ приложена произвольная система сил 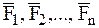 . Выбрав в качестве полюса произвольную точку О СМТ, на основании теоремы о скорости точки СМТ в общем случае движения (Ч.1 Кинематика) скорость движения n-й МТ относительно неподвижной системы координат выразится формулой:
. Выбрав в качестве полюса произвольную точку О СМТ, на основании теоремы о скорости точки СМТ в общем случае движения (Ч.1 Кинематика) скорость движения n-й МТ относительно неподвижной системы координат выразится формулой:
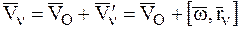 , (4.44)
, (4.44)
где 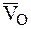 – скорость полюса,
– скорость полюса, 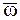 – угловая скорость вращения СМТ вокруг мгновенной оси, проходящей через полюс О.
– угловая скорость вращения СМТ вокруг мгновенной оси, проходящей через полюс О.
Для удобства сначала найдем мощность силы 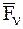 :
:
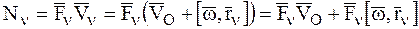 .
.
Второе слагаемое по свойству смешанного произведения и с учетом формулы для момента силы относительно точки (Ч.2 Статика) может быть записано в виде:
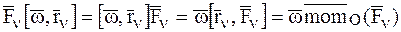 .
.
Подставляя это равенство в предыдущую формулу и используя определение скалярного произведения и связь между моментом силы относительно точки и оси (Ч.1 Статика), получим:
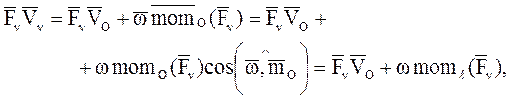
где 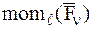 – момент n-й силы относительно мгновенной оси вращения l, проходящей через полюс О.
– момент n-й силы относительно мгновенной оси вращения l, проходящей через полюс О.
Перейдем к определению элементарной работы силы 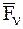 .
.
Учтя соотношения 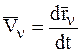 ,
, 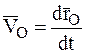 ,
, 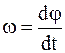 , получим:
, получим:
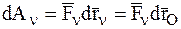 +
+ 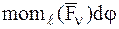 .
.
Тогда элементарная работа всех сил, действующих на СМТ, равна:
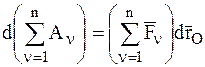 +
+ 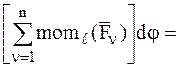
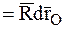 +
+ 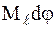 ,
,
где 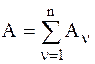 - сумма работ всех сил, действующих на СМТ,
- сумма работ всех сил, действующих на СМТ, 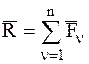 - главный вектор, а
- главный вектор, а 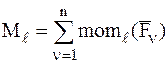 - проекция главного момента на ось l системы сил, действующих на СМТ.
- проекция главного момента на ось l системы сил, действующих на СМТ.
Работа системы сил, действующих на СМТ, примет вид:
А= 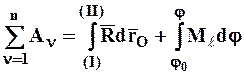 . (4.45)
. (4.45)
В случае поступательного движения НМС соотношение (4.45) примет вид:
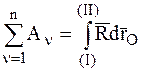 .
.
В случае вращательного движения НМС относительно неподвижной оси z соотношение (4.45) примет вид:
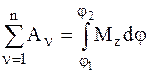 .
.
В случае, когда момент постоянен ( 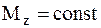 ), его работа выразится формулой:
), его работа выразится формулой:
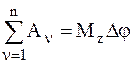 .
.
Дата добавления: 2016-06-05; просмотров: 1812;











