Расчет цепи при произвольной форме воздействия. Интеграл Дюамеля
Предположим, что линейная цепь включается на напряжение 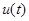 , являющееся произвольной функцией времени. Заменим кривую напряжения ступенчатой линией.
, являющееся произвольной функцией времени. Заменим кривую напряжения ступенчатой линией.
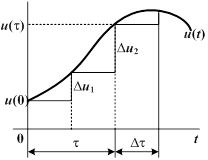
| В этом случае можно считать, что в момент времени 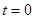 цепь включается на постоянное начальное напряжение цепь включается на постоянное начальное напряжение 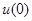 , а затем через равные промежутки времени , а затем через равные промежутки времени 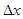 включаются дополнительные источники постоянных напряжений включаются дополнительные источники постоянных напряжений 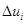 . Эти напряжения в общем случае обладают разной величиной и имеют положительный знак при возрастании напряжения и отрицательный при его убывании. В результате ток в любой ветви при переходном процессе можно найти как сумму токов, вызываемых отдельными постоянными составляющими напряжения. . Эти напряжения в общем случае обладают разной величиной и имеют положительный знак при возрастании напряжения и отрицательный при его убывании. В результате ток в любой ветви при переходном процессе можно найти как сумму токов, вызываемых отдельными постоянными составляющими напряжения.
|
Для применения этого метода необходимо предварительно рассчитать переходный ток исследуемой ветви по заданному постоянному входному напряжению 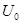 и найти переходную функцию
и найти переходную функцию 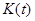 , связывающую искомую и заданную величины. Эта функция зависит от времени и может быть найдена с помощью классического или операторного методов расчета переходного процесса при включении данной цепи под действие постоянного напряжения. При вычислении тока переходная характеристика имеет размерность проводимости и называется переходной проводимостью
, связывающую искомую и заданную величины. Эта функция зависит от времени и может быть найдена с помощью классического или операторного методов расчета переходного процесса при включении данной цепи под действие постоянного напряжения. При вычислении тока переходная характеристика имеет размерность проводимости и называется переходной проводимостью 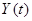 .
.
Если воздействие запаздывает на время t*, то на такое же время запаздывает и реакция цепи. Следовательно, переходная проводимость
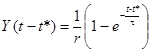 .
.
Составляющая переходного тока от напряжения 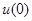 , включаемого в начальный момент, равна
, включаемого в начальный момент, равна 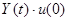 , а от скачка напряжения
, а от скачка напряжения 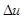 , включаемого в момент
, включаемого в момент 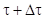 , равняется
, равняется 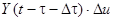 . В результате при переходе
. В результате при переходе 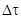 в пределе к бесконечно малым промежуткам времени dτ значение искомого переходного тока будет:
в пределе к бесконечно малым промежуткам времени dτ значение искомого переходного тока будет:
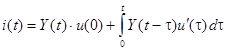
Полученное выражение называется интегралом Дюамеля.
Дата добавления: 2019-12-09; просмотров: 482;











