Энергетические соотношения в цепях синусоидального тока
В цепях постоянного тока и напряжения мощность определялась как
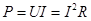 .
.
В цепях синусоидального тока принято говорить о мгновенной мощности цепи.
Мгновенная мощность цепи равна произведению мгновенных значений напряжения и тока:
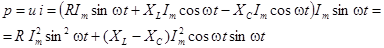
После подстановки значений 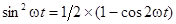 и
и 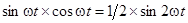 и перехода к действующим значениямвыражение для мгновенной мощности приобретает вид
и перехода к действующим значениямвыражение для мгновенной мощности приобретает вид
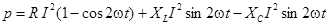
Первый член правой части есть мгновенная мощность активного сопротивления
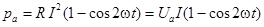
Эта мощность имеет постоянную составляющую 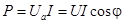 и переменную – синусоиду двойной частоты с такой же амплитудой. Величина Р является, очевидно, средней мощностью за период. Она называется активной мощностью. В системе СИ мгновенная и активная мощности измеряются в ваттах (Вт).
и переменную – синусоиду двойной частоты с такой же амплитудой. Величина Р является, очевидно, средней мощностью за период. Она называется активной мощностью. В системе СИ мгновенная и активная мощности измеряются в ваттах (Вт).
|
Второй и третий член дают мгновенную мощность индуктивности и емкости: 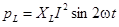 и
и 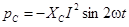
Эти мощности изменяются по синусоидам двойной частоты противоположным по фазе, т. е. когда индуктивность отдает энергию, емкость ее получает, и наоборот. Среднее значение 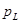 и
и 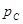 равно нулю. В сумме они дают мгновенную мощность реактивных участков цепи:
равно нулю. В сумме они дают мгновенную мощность реактивных участков цепи: 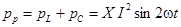 .
.
Амплитуда синусоиды этой мощности 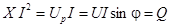 называется реактивной мощностью. В системе СИ реактивная мощность измеряется в реактивных вольт-амперах (вар).
называется реактивной мощностью. В системе СИ реактивная мощность измеряется в реактивных вольт-амперах (вар).
Теперь выражение для мгновенной мощности всей цепи может быть преобразовано:
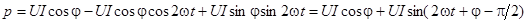 .
.
Таким образом, мгновенная мощность всей цепи имеет постоянную составляющую 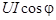 и переменную составляющую – синусоиду с амплитудой
и переменную составляющую – синусоиду с амплитудой 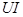 . Мощностьравна нулю, когда и = 0 или i = 0.
. Мощностьравна нулю, когда и = 0 или i = 0.
|
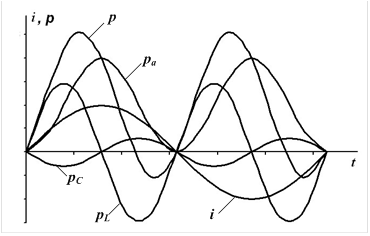
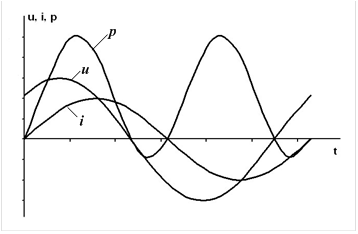
Так как амплитуда переменной части больше постоянной составляющей, мощность в определенные промежутки времени становится отрицательной. Когда мощность положительна, цепь получает энергию от источника; когда мощность отрицательна, цепь отдает энергию источнику. Очевидно, возврат энергии источнику получается за счет энергии поля того из реактивных участков цепи, мощность которого больше (на рисунке за счет индуктивности). Отдавая запасенную в своем поле энергию, индуктивность снабжает энергией емкость, отдает часть своей энергии безвозвратно активному сопротивлению, а остаток возвращает источнику.
Промежутки времени, в течение которых мощность положительна, больше, чем те, при которых мощность отрицательна.
Амплитуда переменной части мгновенной мощности всей цепи 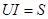 называется полной мощностью и измеряется в системе СИ в вольт-амперах (ва).
называется полной мощностью и измеряется в системе СИ в вольт-амперах (ва).
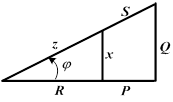
| Если умножить все стороны треугольника сопротивлений на общий множитель 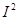 , получается подобный ему прямоугольный треугольник мощностей с гипотенузой, равной полной мощности S катетом, равным активной мощности Р и другим катетом, равным реактивной мощности Q. Из треугольника мощностей видно, что , получается подобный ему прямоугольный треугольник мощностей с гипотенузой, равной полной мощности S катетом, равным активной мощности Р и другим катетом, равным реактивной мощности Q. Из треугольника мощностей видно, что 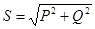 . .
|
Полная мощность S является характерной величиной для всякой электрической установки, любой электрической машины, аппарата, линии передачи и т. п. Сечение их проводов рассчитывается на ток I таким образом, чтобы провода не перегревались от выделяемого в них тепла. Изоляция рассчитывается на напряжение U. Другими словами, любая электрическая установка рассчитывается на полную мощность 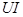 .
.
Полная мощность есть та максимальная активная мощность, которая может быть получена при данных действующих значениях напряжения и тока. Из-за сдвига фаз расчетная (полная) мощность установки используется неполностью. Отсюда ясна важность высокого 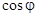 , называемого коэффициентом мощности.
, называемого коэффициентом мощности.
Мощность в комплексной форме
В качестве комплексной мощности принимают произведение комплексного напряжения на сопряженную комплексную величину тока. Получаем в результате такого перемножения комплексную мощность
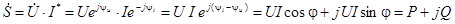 .
.
Вещественная часть равна активной мощности Р, реактивная мощность Q соответствует мнимой части комплексной мощности. Модуль комплексной мощности равен полной мощности 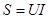 .
.
Баланс мощности
1. Сумма комплексных мощностей для всех ветвей электрической цепи равна 0.
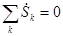 , откуда
, откуда 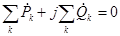 .
.
Такое равенство возможно только в том случае, если 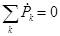 и
и 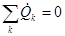 .
.
2. Поскольку в каждой цепи есть источники и приемники, то
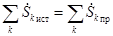
Источники ЭДС и токов можно разделить:
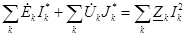 .
.
Действительно, мощность, потребляемую приемником, мы можем представить как:
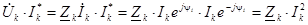 .
.
С другой стороны,
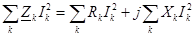
и для мощности источников
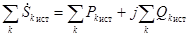
Следовательно, 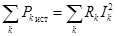 и
и 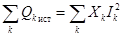 .
.
Дата добавления: 2019-12-09; просмотров: 723;











