Комплексный метод расчета электрических цепей переменного тока

Существенное упрощение достигается изображением синусо­идальных функций времени комплексными числами.

Существует несколько форм представления комплексного числа:

- алгебраическая форма: ;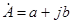

- показательная (или экспоненциальная) форма: ;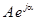

- тригонометрическая форма: .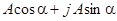

Все эти формы связаны между собой, в частности, модуль числа 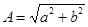, аргумент .

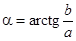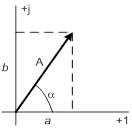
Для геометрического изображения используется прямоугольная система координат, в которой по горизонтальной оси откладываются вещественные числа, а по вертикальной – мнимые. Такая плоскость называется плоскостью Гаусса. , ,

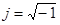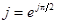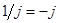
Для вещественной и мнимой частей комплексного числа употреб­ляют также обозначения: , .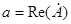

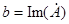Две комплексные величины, имеющие равные модули и равные, но противоположные по знаку аргументы, называют сопря­женными.

Если 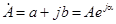, то сопряженное ему комплексное число запишется в форме 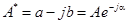. При этом соблюдается равенство: .

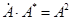Пусть имеется синусоидально изменяющийся ток .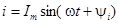

Его можно представить в форме .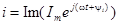

Комплексное число 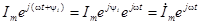будем рассматривать как символическое изображение дейст­вительного синусоидального тока, которое определяется при заданной частоте ω двумя ве­личинами – амплитудой и начальной фазой.

Комплексное число 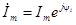называют комплексной амплитудой тока.

Рассмотрим теперь выражение для производной по времени от синусоидального тока

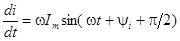
Изображение производной будет иметь вид:

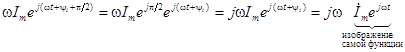
Таким образом, операция дифференцирования действительной функции заменяется умножением на 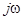ее комплексного изображения.

Рассмотрим изображение интеграла от сину­соидальной функции. В частности, заряд сможет быть найден как

.

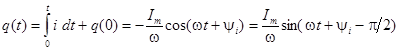(Так как мы рассматриваем только случаи, когда приложенное к зажимам цепи напряжение и э. д. с, действующие в цепи, сину­соидальны и не содержат постоянных составляющих, то напряжения на конденсаторах и заряды на конденсаторах также не содержат постоянных составляющих).

Искомое изображение интеграла будет

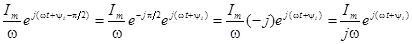
Т. о. операция интегрирования действительной функции заменяется делением на 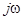ее комплексного изображения.

Таким образом, комплексный метод позволяет заменить интегро-дифференциальное уравнение, содержащее функции времени, алгебраическим уравнением с их комплексными изображениями.

Алгоритм метода:

1. Замена заданных функций времени их комплексными изображениями.

2. Замена всех уравнений, составленных по закону Кирхгофа, алгебраическими уравнениями для комплексных изображений.

3. Нахождение комплексных изображений искомых функций.

4. Переход к оригиналам этих функций.

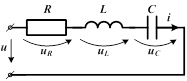
В качестве примера рассмотрим цепь с последовательно соединенными участками R,L и C,к зажимам которой приложено напряжение, изменяющееся по синусоидальному закону .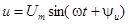

Требуется найти ток в цепи: .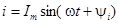

1) В соответствии с алгоритмом заменяем функции времени их изображениями: , .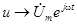

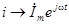2) Составляем уравнение по второму закону Кирхгофа:

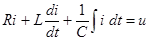и записываем его для комплексных изображений, заменив ток,его производную и интеграл их комплексными выражениями:

.

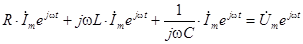Полученное уравнение уже является алгебраическим. Все слагаемые имеют одинаковый множитель 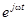, на который уравнение можно поделить. Окончательно получаем уравнение для комплексных амплитуд:

.

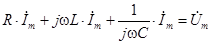Поэтому рассматриваемый метод расчета часто называют методом комплексных амплитуд. В дальнейшем сразу не будем писать множитель 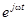, а составлять уравнение для комплексных амплитуд.

3) Из последнего уравнения легко определяется комплексная ам­плитуда тока:

,

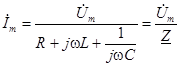где 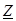– полное комплексное сопротивление цепи.

4) Зная выражение для комплексной амплитуды тока в виде 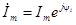, легко записать выражение для мгновенного тока: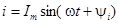

Нас обычно интересуют действующие токи и напряжения. Так как действующие синусоидальные токи и напряжения меньше их амплитуд в 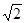, то обычно вместо комплексных амплитуд рассмат­ривают комплексные действующие величины: , .

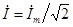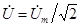Комплексные сопротивление и проводимость

Отношение комплексного напряжения к комплексному току называют комплексным сопротивлением цепи и обозначают .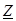

,

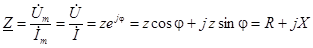где 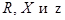– активное, реактивное и полное сопротивления цепи.

В частности, для последовательного соединения R,L и C

.

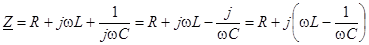Аналогично, отношение комплексного тока к комплексному напряжению называют комплексной проводимостью цепи и обозначают 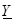. Имеем:

,

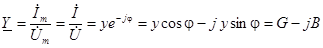где 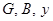– активная, реактивная и полная проводимости цепи.

Для параллельного соединения трех элементов

.

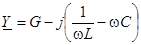Очевидно, существует связь: 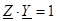или

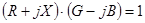
Основные законы электрических цепей в комплексной форме

Вид законов электрических цепей переменного тока в комплексной форме такой же, как и для цепи постоянного тока. Только необходимо произвести замену соответствующих постоянных величин комплексными: , , , , , .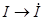

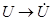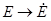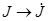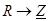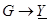Закон Ома в комплексной форме имеют вид: .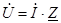

Достоинство этих выражений заключается в том, что в них учи­тывается как связь между действующими значениями тока и напряжения,так и сдвиг фаз между ними.

Первый закон Кирхгофа в применении к узлу цепи .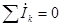

Второй закон Кирхгофа применительно к контуру цепи .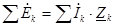

Возможность использовать соотношения для цепей постоянного тока справедлива и для эквивалентных преобразований.

При последовательном соединении участков цепи напряжение на зажимах всей цепи равняется сумме падений напряжений на отдельных участках.Следовательно, при после­довательном соединении комп­лексное сопротивление всей цепи равно алгебраической сумме комплексных сопротивлений от­дельных участков цепи: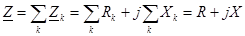

При параллельном соединении участков цепи общий ток на входе цепи равен сумме токов в отдельных участках. Таким образом, при параллельном соединении комплексная проводимость всей цепи равна алгебраической сумме комплексных проводимостей отдельных участков цепи:

.

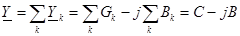При смешанном соединении:

; , . , , .

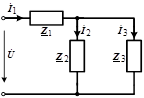
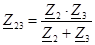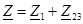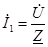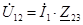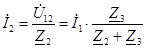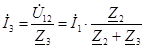Расчет сложных цепей переменного тока комплексным методом осуществляется с помощью тех же методов, что и цепей постоянного тока при замене соответствующих величин их комплексными аналогами.