Резонансы в электрических цепях синусоидального тока
Индуктивные и емкостные сопротивления, а также индуктивные и емкостные проводимости могут взаимно компенсироваться. В результате ток в цепи будет совпадать по фазе с напряжением, приложенным к зажимам этой цепи. Т.е. несмотря на наличие реактивных сопротивлений, взятая в целом цепь, ведет себя как активное сопротивление. В этом случае говорят, что в цепи существует резонанс.
Колебательными или резонансными называются электрические цепи, в которых могут возникать явления резонанса напряжения или тока.
Резонанс напряжений наблюдается в цепи с последовательным соединением R, L, C. При резонансе напряжений на зажимах цепи имеем 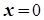 .
.
Резонанс токов наблюдается в цепи с параллельным соединением R, L, C. При резонансе тока на зажимах цепи имеем 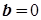 .
.
Частоты, при которых наблюдается явление резонанса, называются резонансными частотами.
Резонанс в последовательном колебательном контуре (резонанс напряжений)
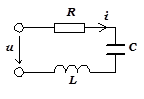
| Рассмотрим последовательный колебательный контур.В такой цепи полное входное сопротивление можно записать как
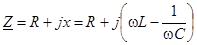 . .
|
Условие резонанса в такой цепи означает: 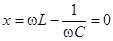 .
.
В этом случае ток совпадает по фазе с напряжением, угол сдвига фаз 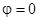 .
.
Рассмотрим векторную диаграмму цепи при резонансе. Угловую частоту, при которой наступает резонанс, называют резонансной или собственной угловой частотой цепи. Из условия резонанса: 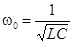
| 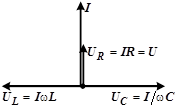
|
Вектор приложенного к цепи напряжения при резонансе совпадает с вектором падения напряжения на активном сопротивлении. При этом напряжения на индуктивности и емкости могут значительно превышать напряжение на зажимах цепи. Поэтому резонанс при последовательном соединении называют резонансом напряжений.
Превышение напряжения на реактивных элементах цепи над напряжением на зажимах цепи имеет место, если 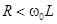 Ю что сводится к одному:
Ю что сводится к одному:
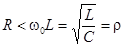 .
.
Эта величина имеет размерность сопротивления и называется характеристическим или волновым сопротивлением контура.
Кратность перенапряжения на реактивном элементе, т.е. определяется отношением: 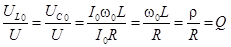 .
.
При резонансе эту величину называют добротностью контура.
Величина, обратная добротности 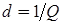 , определяет затухание контура.
, определяет затухание контура.
Рассмотрим, что происходит в последовательном колебательном контуре с электромагнитной энергией. При этом будем считать, что имеют место синусоидальные воздействия:
ток 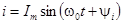 ,
,
напряжение на емкости 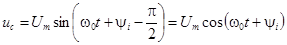
В режиме резонанса 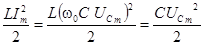
Тогда электромагнитная энергия может быть записана в виде:
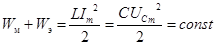
Т.о. при резонансе сумма энергий магнитного и электрического полей с течением времени не изменяется.
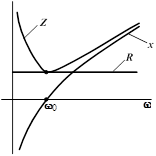
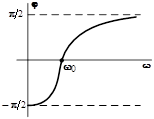
Частотные характеристики последовательного R-L-C контура
Зависимости параметров цепи ( 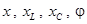 и т.д.) от частоты (
и т.д.) от частоты ( 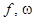 ) называются частотными характеристиками.
) называются частотными характеристиками.
| 
| 
|
Резонансные характеристики
Действующее значение тока в последовательном резонансном контуре:
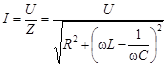 .
.
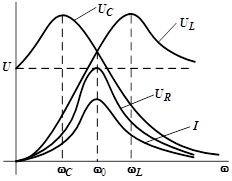
Построим зависимости напряжений на элементах контура от частоты при поддержании на зажимах цепи постоянного напряжения.
| Падение напряжения на индуктивности: 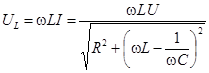 ;
на емкости: ;
на емкости: 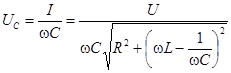 . .
|
Имеет место симметрия максимумов кривых напряжения на реактивных элементах: 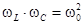
Резонанс в параллельном колебательном контуре (резонанс токов)
Рассмотрим цепь, состоящую из параллельно включенных активного, индуктивного и емкостного сопротивлений.
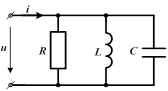
| Для этой цепи полная комплексная проводимость
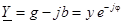 , , 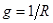 ,
угол сдвига фаз ,
угол сдвига фаз 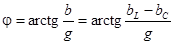 ,
модуль проводимости ,
модуль проводимости 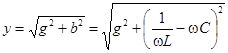
|
Из этого выражения видно, что взаимная компенсация реактивных проводимостей (т.е. 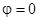 ) достигается при условии:
) достигается при условии: 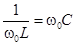 ,
,
т.е. при том же условии, при котором имеет место резонанс напряжений.
Резонансная частота так же определяется выражением вида: 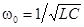 .
.
При резонансе реактивная проводимость цепи равна нулю, поэтому полная проводимость достигает минимального значения. Поэтому ток в общей ветви при неизменном напряжении на зажимах цепи имеет наименьшее значение.
Векторная диаграмма при резонансе имеет вид:
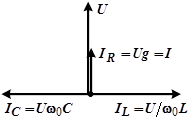
| Вектор тока в общей ветви является геометрической суммой векторов трех токов, два из которых IL и IC находятся в противофазе. Следовательно, возможны случаи, когда токи в индуктивной катушке и конденсаторе будут значительно превосходить суммарный ток в цепи. Поэтому резонанс при параллельном соединении называют резонансом токов. |
Энергетические процессы в параллельной цепи аналогичны соответствующим процессам в последовательной цепи, т.е. и в этом случае происходят колебания энергии в цепи. Энергия полей переходит из конденсатора в катушку и обратно. Источник энергии покрывает потери энергии в ветви с активной проводимостью.
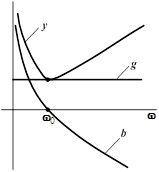
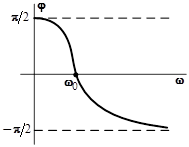
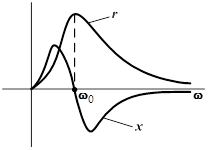
Частотные характеристики цепи с параллельным соединением элементов.
| 
| 
|
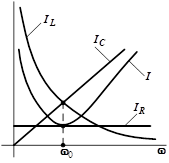
Резонансные кривые при параллельном соединении элементов

| 
|
| режим постоянного тока от источника | режим постоянного напряжения |
Дата добавления: 2019-12-09; просмотров: 681;











