Вопрос 2. Эффект Комптона.

В 1923 г. А. Комптон, исследуя рассеяние рентгеновских лучей разными веществами, обнаружил, что в рассеянных лучах наряду с излучением первоначальной длины волны 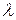содержатся также лучи большей длины волны .

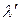Разность 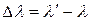оказалась зависящей только от угла 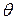, образуемого направлением рассеянного пучка. От длины волны λ и от природы рассеивающего вещества Δλ не зависит.

Все особенности эффекта Комптона можно объяснить, рассматривая рассеяние как процесс упругого столкновения рентгеновских фотонов с практически свободными электронами. Энергия связи с атомом таких электронов мала по сравнению с энергией, передаваемой ему рентгеновским квантом при столкновении.

Вычислим энергетические потери фотона при взаимодействии с электроном. Воспользуемся законами сохранения их полной энергии и полного импульса, подобно как для двух упруго взаимодействующих шаров.

Пусть 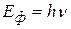– энергия фотона до столкновения,

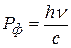– модуль импульса фотона до столкновения,

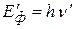– энергия фотона после столкновения,

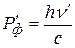– модуль импульс фотона после столкновения,

тогда 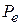– модуль импульс электрона до столкновения,

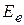– полная энергия электрона до столкновения,

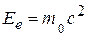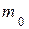, – масса покоя электрона,

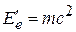– полная энергия движущегося электрона.

Согласно закону сохранения энергии:

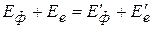. (18.8)

Закон сохранения импульса запишется в виде:

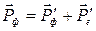. (18.9)

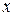Спроектируем векторное уравнение (18.9) на координатные оси и 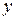(рис. 18.4):

Рис. 18.4

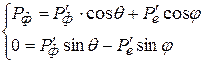. (18.10)

Исключим угол 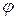из системы уравнений (18.10). Для этого в левые части уравнений перенесём слагаемые, содержащие угол 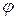, и возведём полученные уравнения в квадрат:

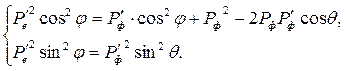
После сложения уравнений получим:

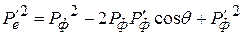. (18.11)

Уравнения (18.8) и (18.11) запишем в явном виде:

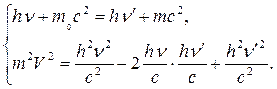(18.12)

Из первого уравнения системы (18.12) выразим 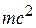и возведем в квадрат получившееся уравнение, а второе уравнение этой системы умножим на :

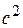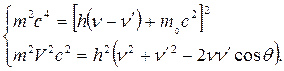
Из первого уравнения вновь полученной системы вычтем второе:

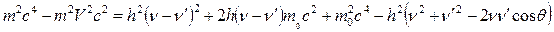. (18.13)

Т.к. 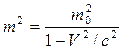и 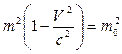, то левая часть уравнения (18.13) приводится к виду:

.

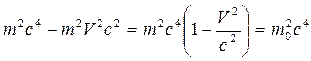После преобразования правой части уравнение приобретает вид:

,

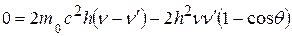или 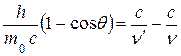, т.к. 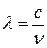, то

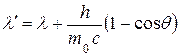. (18.14)

Пусть 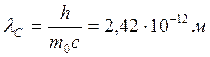, (18.15)

тогда 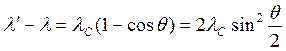. (18.16)

Из приведенного уравнения (18.16) следует, что комптоновская длина волны λ_C представляет собой изменение длины волны фотона при его рассеянии на угол .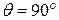

Комптоновская длина волны аналогично вводится для протона, нейтрона и других элементарных частиц. Она определяется выражением (18.15) при замене массы покоя электрона на массу покоя соответствующей частицы.

Эффект Комптона подтвердил правильность квантовых представлений об электромагнитном излучении как о потоке фотонов и может рассматриваться как упругое столкновение двух частиц – фотона и электрона, при котором фотон передает электрону часть своей энергии (и импульса), вследствие чего его частота уменьшается, а длина волны увеличивается.

В наших рассуждениях электрон, на котором рассеивался фотон, предполагается неподвижным. Упругое рассеяние фотонов на высокоэнергичных подвижных электронах может привести к ситуации, приводящей к увеличению энергии и частоты фотонов (уменьшению длины волны). Это явление называется обратным эффектом Комптона.