Поток отказов N восстанавливаемых обьектов.

Число отказов какого-то j-го объекта на i-м интервале - k_ij, гдеi-номер интервала, например - № 7 - июль-месяц; j-номер реализации, то есть порядковый номер объекта в рассматриваемой партии (один из N).

Для i-го интервала определим среднее число отказов, приходящееся на один объект

N

k_срi = 1/N åk_ij. (6-1)

j=1

Математическое ожидание этой величины

N

M[k_i] = m_i = Lim[(1/N) åk_ij] = Lim(k_срi) (6-2)

N→∞ j=1 N→∞

Перейдем от интервалов к реальному времени t_i = ∆t i. За это время будет какое-то количество отказов. Нас интересует количество отказов на один объект, а во-вторых – математическое ожидание этой величины, то есть сумма математических ожиданий m_i, изменяющаяся во времени.

t

Ω(t) = å m(∆t_i)(6-3)

Эта величина называется ведущей функцией объекта. Ведущая

функция - математическое ожидание суммарного количества отказов объекта с начала эксплуатации до рассматриваемого момента времени.

Так как число отказов не может быть отрицательным, то ведущая функция - неубывающая функция времени.

Если на графике этой неубывающей функции времени выделить прямые участки (или спрямить), то угол наклона графика Ω(t) к осиt будет разным. Больший наклон будет означать нестационарность потока отказов (рисунок 6.2).

Ω(t)

Грозы

Гололед

М[k_i]

∆t_i t

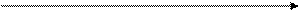
Рис. 6.2