Отказы испытуемых изделий в течение времени работы

Статистическая оценка вероятности отказа - отношение числа отказавших изделий n(t)к общему числу изделий, поставленных на испытания

N(t)

q^*(t) = ------(2-18)

N(0)

Статистическая оценка условной ВБР

р^*(t+∆t) N(t+∆t)

р^*(t,t+∆t) = --------- = --------(2-19)

Р^*(t) N(t)

Наибольший интерес представляет статистическая оценка условной вероятности отказа

q^*(t,t+∆t) = 1 - Р^*(t,t+∆t) =

N(t+∆t) N(t) - N(t+∆t)

= 1 - --------- = 1 - --------------- =

N(t) N(t) (2-20)

n(t+∆t) - n(t) ∆n(t,t+∆t)

= -------------- = ------------ .

N(t) N(t)

Связь между двумя формами представления ВБР и вероятности

отказов следующая. Если бы мы включили в работу бесконечное число

однотипных исправных испытуемых изделий, то есть N(0) = ∞, то теоретическая ВБР совпала бы со статистической (то же самое и вероятность отказа). На практике это совпадение будет тем ближе, чем больше будет взято число N(0).

ЧАСТОТА ОТКАЗОВ

Вероятностное определение

Частота отказов - это производная по времени от вероятности отказа

а(t) = q’(t).(2-23)

Зная частоту отказов, можно определить вероятность отказа.

t

q(t) = ∫а(t)dt(2-24)

В теории вероятностей кроме понятия функции распределения случайной величины существует понятие плотности распределения. Это производная по значению случайной величины (у нас по времени) от функции распределения этой случайной величины.

В случае нашей случайной величины - наработки до отказа Т-

- частота отказов как раз и будет представлять собой плотность распределения наработки до отказа.

а(t) = q’(t) = f(t). 2-25)

Зависимости вероятности и частоты отказов от времени представлены на рисунке 2.4.

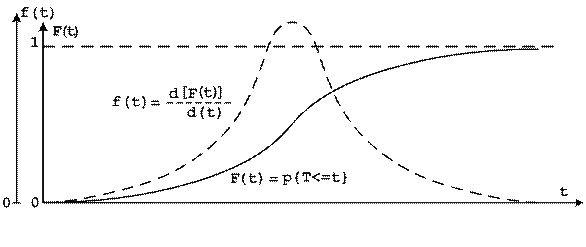
Рис 2.4.

Частота и вероятность отказов