ЭКСПОНЕНЦИАЛЬНЫЙ ЗАКОН РАСПРЕДЕЛЕНИЯ

При экспоненциальном (показательном) распределении наработки до отказа функция распределения НДО и ВБР имеют вид

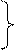q(t) = F(t) = 1 - Exp(-lt), а

р(t) = е^-lt, (3-1)

где l - константа, параметр экспоненциального распределения.

Плотность распределения НДО определим как производную от вероятности отказа

f(t) = q¢(t) = [1- Exp(-lt)]¢ =

= (-l)t)[- Exp(-lt)] = l Exp(-lt)(3-2)

Интенсивность отказов определится как отношение плотности распределения к ВБР

l(t) = f(t)/p(t) = l Exp(-lt)/Exp(-lt) = l.(3-3)

Главной особенностью экспоненциального закона распределения НДО является независимость от времени интенсивности отказовl. Наоборот, если известно, что l = Сonst, то это означает, что имеет место экспоненциальный закон распределения наработки до отказа Т.

CНДО определим по выражению (2-32)

∞ ∞

Т_ср = ∫p(t)dt = ∫Exp(-lt)dt =

0 0

∞(3-4)

= 1/(-l) Exp(-lt)ê = 1/(-l)(0 - 1) = 1/l.

Таким образом, средняя наработка до отказа при экспоненциальном законе распределения НДО представляет собой величину, обратную интенсивности отказов.

Т_ср = -----(3-4)

l

При исследовании надёжности изделий экспоненциальное распределение применяется чаще других. Можно назвать три причины такого применения:

1. Экспоненциальное распределение НДО типично для сложных объектов, состоящих из многих элементов с разными распределениями их НДО. Кроме того, для многих объектов можно «снять приработку» (см. рис. 1.4), и интенсивность отказов можно считать постоянной.

2. При этом законе простые выражения, с ними легче работать.

3. При ограниченных возможностях экспериментальных исследований принимают l=Const в качестве первого приближения, когда ничего другого предположить нельзя по причине нехватки информации.