Некогерентный приём

На практике иногда не удается обеспечить условия для когерентного приема сигналов, так как один или несколько параметров принимаемого сигнала оказываются неизвестными. Такая ситуация типична, например, для систем спутниковой связи, радиосвязи с подвижными объектами, и т.п., поскольку расстояние между передатчиком и приемником изменяется случайным образом. Это приводит, в частности, к тому, что меняется начальная фаза несущего колебания.

Если изменение происходит настолько медленно, что соседние посылки имеют практически одинаковую начальную фазу, то ее можно оценить и оценку использовать вместо точного значения при организации приема. Такой прием называют квазикогерентным.

Если же начальная фаза изменяется (флюктуирует) быстро или устройство оценивания оказывается слишком сложным, тогда рассматривается задача приема сигнала со случайной начальной фазой, или некогерентного приема.

Перепишем выражение (17.7) для логарифма отношения правдоподобия при приеме сигнала s(t):

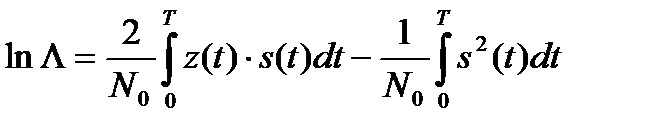. (17.18)

Сигнал при некогерентном приеме известен с точностью до начальной фазы, поэтому обозначим его s(t, φ) и запишем .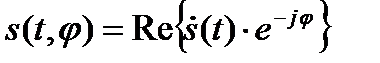

В этом выражении неизвестная начальная фаза сигнала представлена комплексным фазовым множителем e^-jφ при аналитическом комплексном сигнале, который определяется выражением 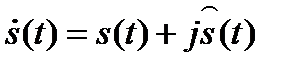, где вещественная и мнимая части связаны парой преобразований Гильберта

,

.

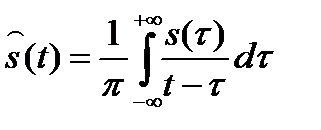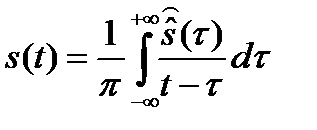Тогда,

.

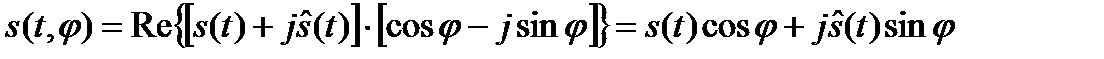Корреляционный интеграл в выражении (17.18) в таком случае приобретает вид

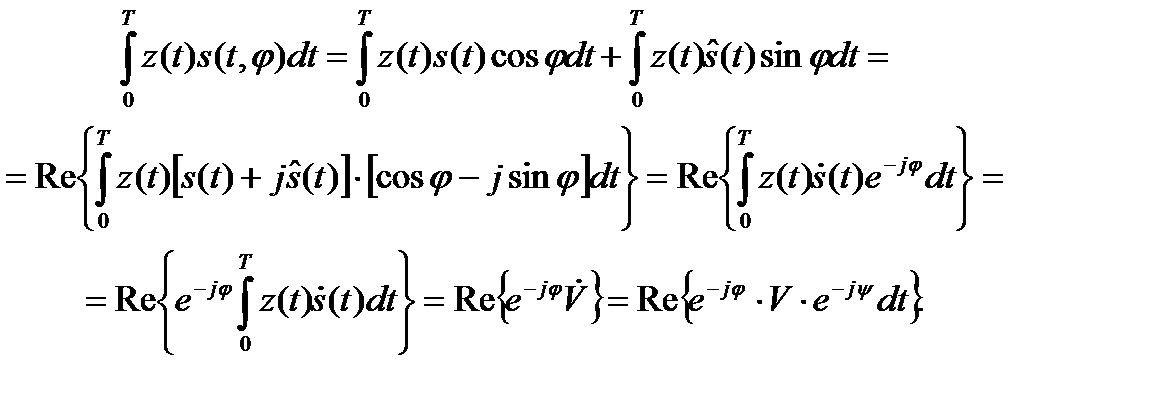(17.19)

В полученном выражении фигурирует комплексная величина 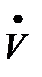, имеющая смысл корреляционного интеграла для аналитического сигнала s(t):

,

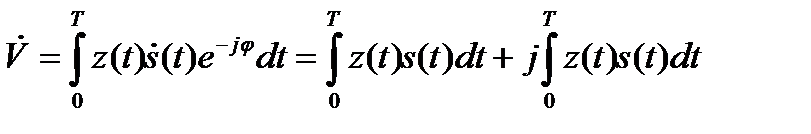где

;

.

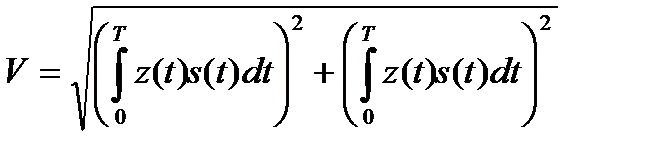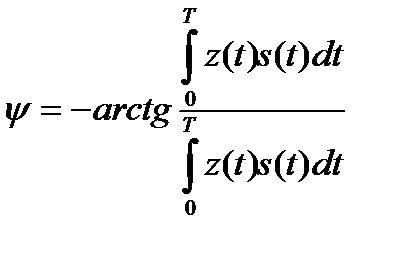Корреляционный интеграл согласно (17.19) можно переписать в виде

,

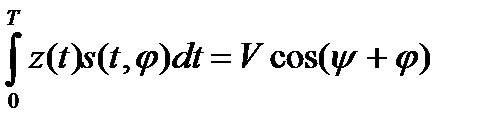тогда логарифм отношения правдоподобия

,

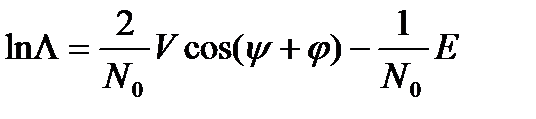а само отношение правдоподобия

.

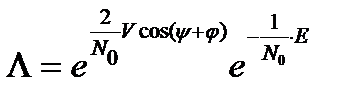Считая, что начальная фаза сигнала является случайной величиной, имеющей равномерное в интервале (0, 2π) распределение, выполним усреднение отношения правдоподобия по ансамблю:

.

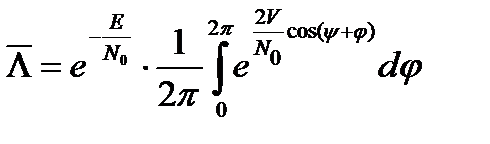Учтём известное соотношение

,

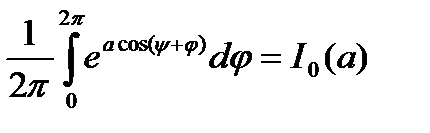где I₀(a) – модифицированная функция Бесселя нулевого порядка, тогда

.

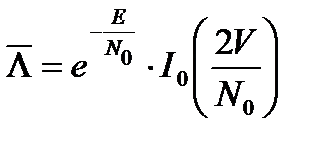Правило некогерентного приема сигнала со случайной равновероятной начальной фазой на фоне гауссовского шума должно быть основано на сравнении величины 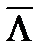с некоторым порогом, а правило различения двух сигналов – на сравнении двух отношений правдоподобия между собой. Предположим, что рассматривается прием двух сигналов s₁(t) и s₀(t). Сравнение усредненных отношений правдоподобия можно заменить сравнением их логарифмов

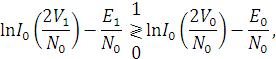
или сравнением с порогом разности логарифмов

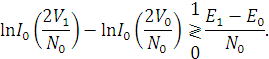
Алгоритм сильно упрощается, если энергии сигналов равны, в этом случае в силу монотонности функции I₀ можно сравнивать между собой величины:

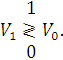
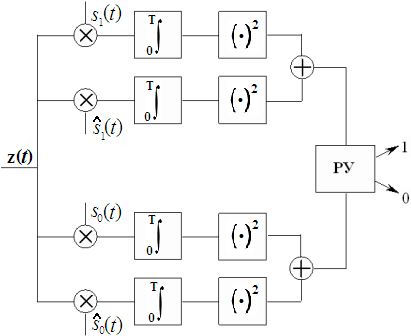
Рис. 17.8. Структура некогерентного приемника двух сигналов с равными энергиями

То же правило можно реализовать с использованием согласованных фильтров по схеме, рисунок 17.9. Здесь вычисление величин V₁ и V₀ производится устройством, называемым детектором огибающей ДО.

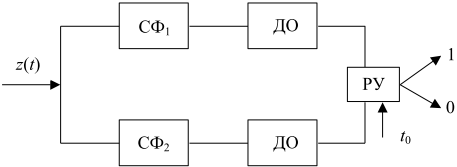
Рис. 17.9. Структура некогерентного приемника двух сигналов с использованием согласованных фильтров