Потенциальная помехоустойчивость когерентного приёма
По определению В.А. Котельникова потенциальной помехоустойчивостью называется максимум вероятности правильного решения, достижимый при заданных условиях приема сигналов на фоне помех (шумов) [13].
Определим потенциальную помехоустойчивость приёма двух сигналов, s0(t) и s1(t) известной формы на фоне белого гауссовского шума при равных априорных вероятностях сигналов.
Алгоритм принятия решения в приемнике, реализующем критерий максимума правдоподобия, кратко запишем в виде
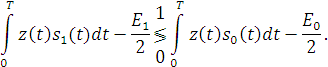
Это выражение можно привести к виду
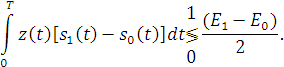
Ошибки при приеме состоят в том, что при передаче первого сигнала принимается решение о приеме второго и наоборот, поскольку гауссово распределение симметрично и априорные вероятности равны.
Найдем условную вероятность ошибки, т.е. вероятность события, заключающегося в принятии решения о наличии сигнала s0(t) при условии, что в наблюдаемом колебании присутствует сигнал s1(t). Это событие соответствует выполнению неравенства
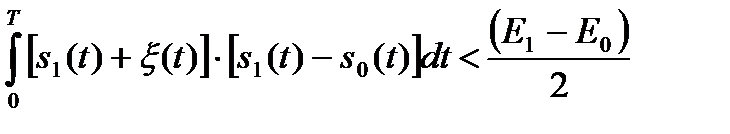 ,
,
которое можно переписать в виде
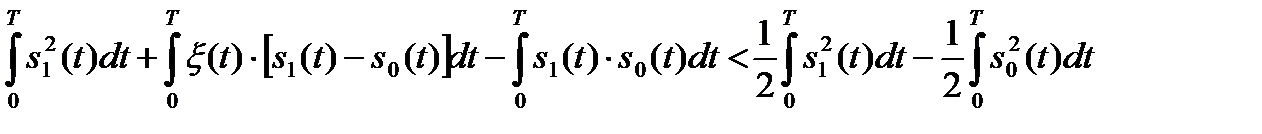 .
.
Проведя очевидные преобразования, получим
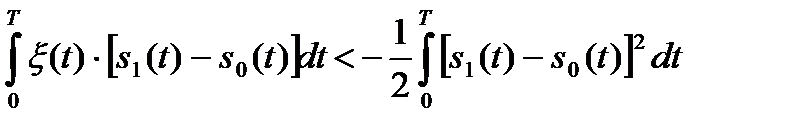 . (17.16)
. (17.16)
Левая часть неравенства представляет собой случайную величину (т.к. это интеграл по времени от случайного процесса ξ(t) с весом, равным разности сигналов sΔ(t) = [s1(t) - s0(t)]), имеющую нормальное распределение (поскольку процесс ξ(t) гауссов) с нулевым средним; обозначим ее v, её дисперсия (средний квадрат), равна:
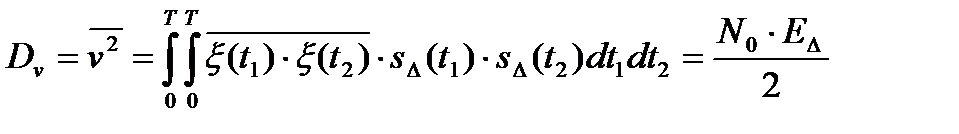 . (17.17)
. (17.17)
Вероятность выполнения неравенства (17.16) – это вероятность того, что нормальная случайная величина с нулевым средним и дисперсией N0EΔ/2 принимает значение меньше, чем EΔ/2. Эта вероятность равна
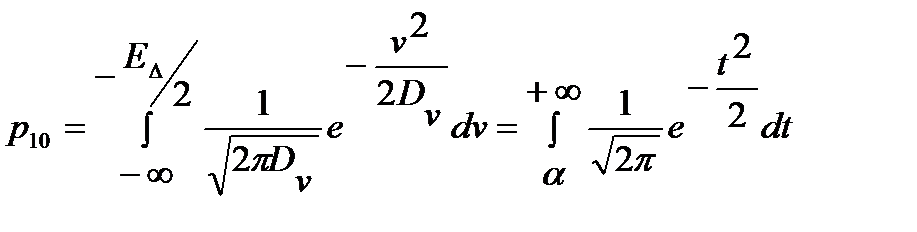 ,
,
где 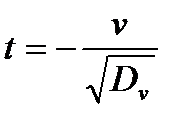 – центрированная нормальная случайная величина с единичной дисперсией, а
– центрированная нормальная случайная величина с единичной дисперсией, а 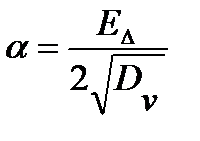 – положительное число.
– положительное число.
Очевидно, p10 зависит только от 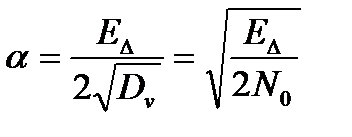 , поэтому можно ввести функцию
, поэтому можно ввести функцию
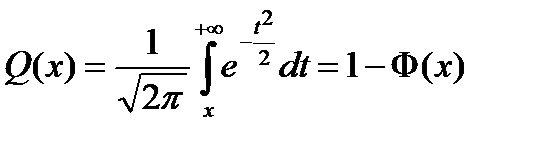 ,
,
где 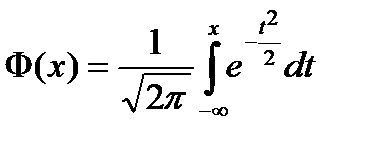 – интеграл вероятности, и записать
– интеграл вероятности, и записать 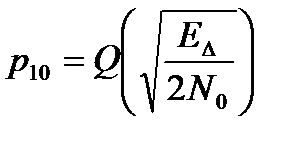 .
.
(Напомним, что в силу симметрии гауссовского распределения p10 = p01).
Таким образом, условная вероятность ошибки, равная средней вероятности ошибки при когерентном приеме сигналов на фоне белого шума, определяется энергией разностного сигнала sΔ(t) и спектральной плотностью мощности шума N0.
Рассмотрим потенциальную помехоустойчивость двоичного когерентного приемника максимального правдоподобия для различных способов модуляции, считая, что энергия сигнала E фиксирована.
Представляет практический интерес сравнительная оценка потенциальной помехоустойчивости сигналов дискретной модуляции: амплитудной (ДАМ), частотной (ДЧМ), фазовой (ДФМ).
При ДАМ символу «1» соответствует сигнал S1(t), а символу «0» соответствует сигнал S2(t) = 0 («пассивная пауза»), следовательно норма разностного сигнала равна
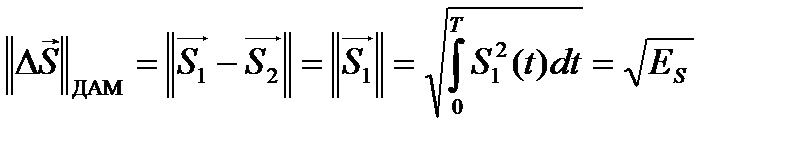 .
.
При ДЧМ и ДФМ символам «1» и «0» соответствуют сигналы S1(t) и S2(t), энергия которых одинакова. При этом для нормы разностного сигнала имеем
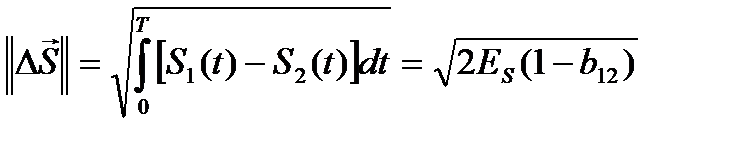 ;
;
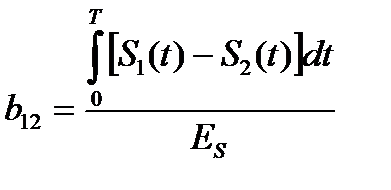 , где b12 – нормированный коэффициент корреляции (-1 ≤ b12 ≤ 1).
, где b12 – нормированный коэффициент корреляции (-1 ≤ b12 ≤ 1).
В частности, для ортогональных сигналов ДЧМ
b12 = 0, 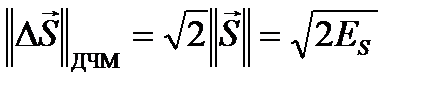 ,
,
а для противоположных сигналов ДФМ
b12 = -1, 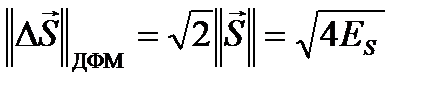 .
.
Сигналы с b12 = 1 являются одинаковыми, т.е., и их невозможно различить. Для них Рош = 0,5, что эквивалентно обрыву канала связи.
Т.о. энергия разностного сигнала 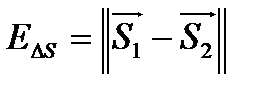 для ДЧМ в 2 раза, а для ДФМ – в 4 раза больше по сравнению с ДАМ. Соответственно возрастает и помехоустойчивость.
для ДЧМ в 2 раза, а для ДФМ – в 4 раза больше по сравнению с ДАМ. Соответственно возрастает и помехоустойчивость.
Заметим, что если используются три сигнала одинаковой энергии, то для достижения максимальной помехоустойчивости они должны иметь взаимный фазовый сдвиг 1200, т.е. соответствующие сигналам точки должны располагаться на окружности радиуса E1/2 в вершинах равностороннего треугольника (рис. 17.7.г). Если сигналов четыре, то оптимальным является их размещение в вершинах правильного тетраэдра, вписанного в сферу радиуса E1/2.
В общем случае оптимальный выбор системы из n сигналов соответствует их расположению в вершинах правильного (n - 1) – мерного симплекса, вписанного в (n - 1) – мерную сферу (отрезок, треугольник и тетраэдр являются одномерным, двумерным и трехмерным симплексами).
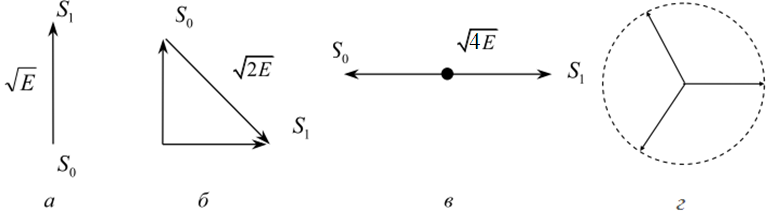
Рис. 17.7. К помехоустойчивости приема двух и трёх сигналов
Дата добавления: 2017-10-04; просмотров: 2469;











