Потенциальная помехоустойчивость некогерентного приёма
Определим потенциальную помехоустойчивость некогерентного приема на примере системы с пассивной паузой при равных априорных вероятностях посылок
s1(t) = A cos(ωt + φ), s0(t) = 0, p1 = p0 = 0,5.
Средняя вероятность ошибки равна
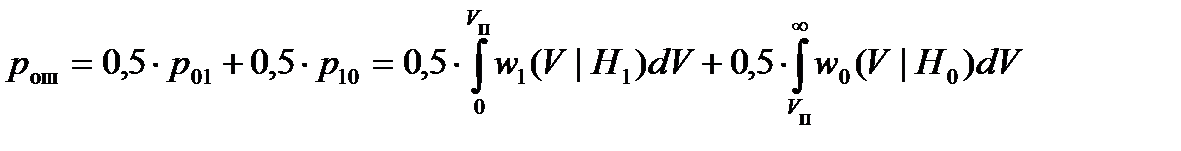 .
.
Здесь w1(V|H1) и w0(V|H0) – условные плотности распределения вероятности огибающей корреляционного интеграла при условии принятия гипотез о передаче сигналов s1(t) и s0(t) соответственно, Vп – порог (рис. 17.10).
При гипотезе H0 значение огибающей обусловлено только шумом, тогда квадратурные составляющие являются независимыми нормальными случайными величинами с нулевыми средними и дисперсиями N0E/2 (см. выражение 17.17).
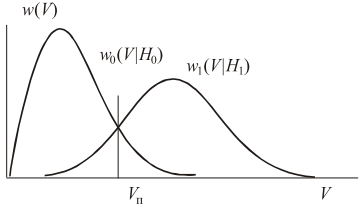
Рис. 17.10. Выбор порога при некогерентном приеме
Условная плотность распределения вероятностей огибающей имеет рэлеевский вид
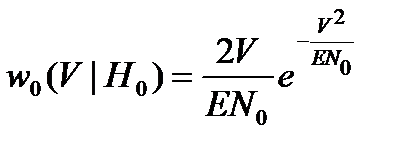 .
.
Если наблюдаемое колебание содержит сигнал s1(t), то огибающая имеет обобщенное рэлеевское распределение (распределение Рэлея-Райса)
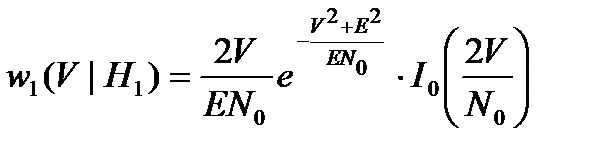 .
.
Средняя вероятность ошибки равна
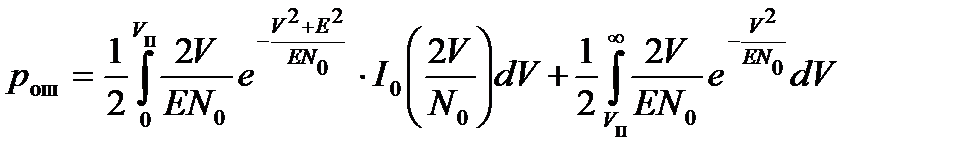 . (17.20)
. (17.20)
Второй интеграл берется по частям, при этом
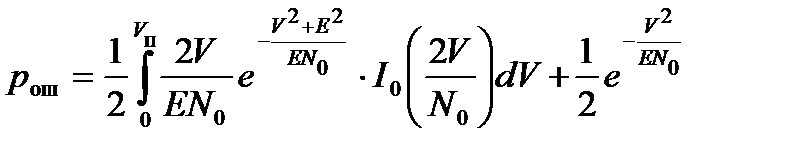 .
.
Оптимальное значение порога, при котором достигается потенциальная помехоустойчивость некогерентного приема, является решением уравнения dpош/dVп = 0. Точно решить полученное уравнение не удается. Поэтому оптимальный порог определяется приближенными выражениями

Подставляя в (17.20) порог E/2, получим среднюю вероятность ошибки при больших отношениях сигнал/шум (ОСШ):
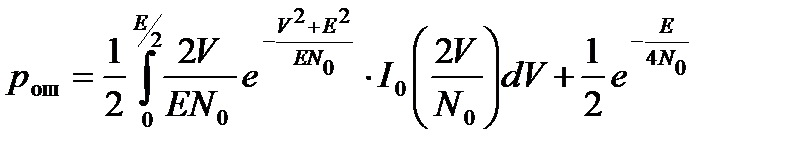
При больших ОСШ (E/N0 ≥ 10) первым слагаемым можно пренебречь, тогда
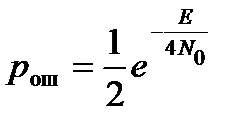 .
.
Аналогично можно проанализировать помехоустойчивость приема двух ортогональных частотно-манипулированных сигналов; для этого случая средняя вероятность ошибки
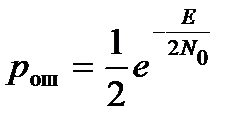 .
.
Сигналы с фазовой манипуляцией при случайной начальной фазе каждой посылки применять при некогерентном приеме нельзя. Однако при медленных изменениях фазы можно использовать относительную фазовую манипуляцию, при которой начальная фаза следующей посылки совпадает с начальной фазой предыдущей посылки при передаче символа «0» и отличается от нее на 1800 – при передаче символа «1». При этом средняя вероятность ошибки
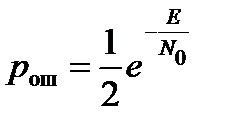 .
.
Дата добавления: 2017-10-04; просмотров: 1878;











