Приём полностью известного сигнала (когерентный приём)
Рассмотрим принятие решения в системе связи при следующих условиях: синхронизация является точной и форма сигнала на интервале наблюдения точно известна, неизвестен лишь сам факт наличия либо отсутствия сигнала в наблюдаемом колебании. (Эта ситуация наиболее близка к реальности в кабельных линиях связи, где условия распространения сигналов известны и практически неизменны.)
Будем считать, что на интервале наблюдения независимо от сигнала присутствует гауссовский шум с нулевым средним значением и спектральной плотностью мощности N0/2, постоянной в некоторой полосе частот -F < f < F («квазибелый» шум).
Полагая, что длительность интервала наблюдения равна T, возьмем n отсчетов наблюдаемого колебания с шагом Δt = 1/2F = T / n, при этом отсчеты шума являются некоррелированными вследствие того, что корреляционная функция квазибелого шума (вида "sin x / x") пересекает ось абсцисс при значениях времени, кратных Δt. Поэтому совместная плотность распределения вероятностей взятых отсчетов (выборочных значений) в отсутствие сигнала равна:
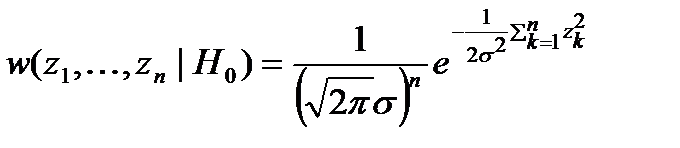 ,
,
где σ2 = N0 / F = N0 / 2Δt.
Если сигнал присутствует и принимает в моменты взятия отсчетов значения sk = s(tk), то совместная плотность распределения вероятностей выборочных значений
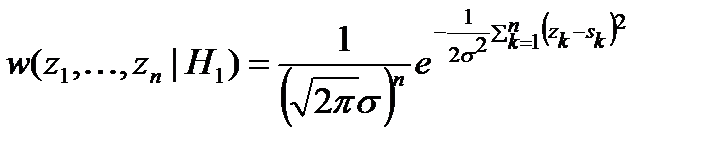 .
.
Отношение правдоподобия
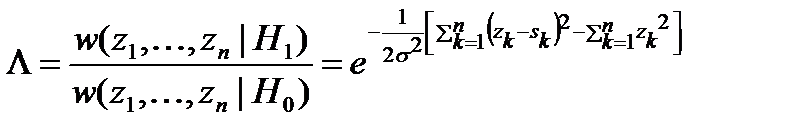 .
.
Подставляя в это выражение 2σ2 = N0 / Δt, получим
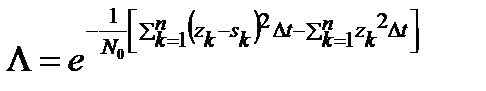 . (17.6)
. (17.6)
Устремляя Δt к нулю (n→∞), запишем логарифм отношения правдоподобия:
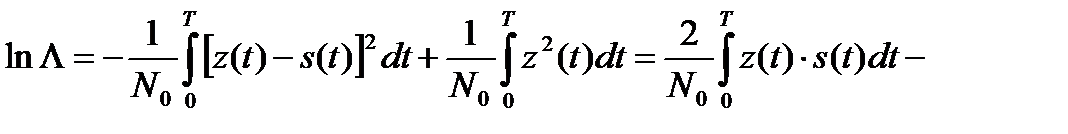
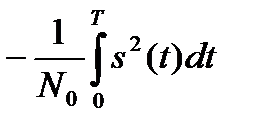 . (17.7)
. (17.7)
Поскольку логарифм является монотонной функцией, правило обнаружения сигнала известной формы на фоне гауссовского квазибелого шума, оптимальное по критерию максимума правдоподобия, основано на сравнении с нулевым порогом величины
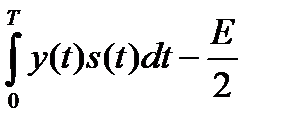 , (17.8)
, (17.8)
где 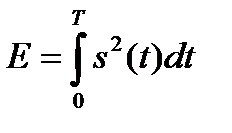 – энергия сигнала.
– энергия сигнала.
Первое слагаемое в выражении (17.8) называется корреляционным интегралом, так как совпадает по форме с выражением взаимно корреляционной функции сигнала и наблюдаемого процесса при нулевом сдвиге. Энергия сигнала известна, и при обнаружении можно сравнивать значение корреляционного интеграла (случайное в силу случайности реализации z(t)) с порогом, равным E/2.
Правило различения M сигналов известной формы на фоне гауссовского квазибелого шума, оптимальное по критерию максимума правдоподобия, основано на сравнении между собой величин 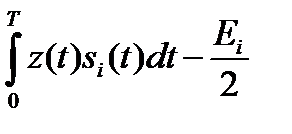 , i = 1,… M.
, i = 1,… M.
Решение принимается в пользу того сигнала, для которого эта величина максимальна.
Структура оптимального приемника для различения M сигналов показана на рисунке 17.3.
Устройство выбора максимума УВМ выдает на выход номер k канала, в котором величина (17.8) максимальна.
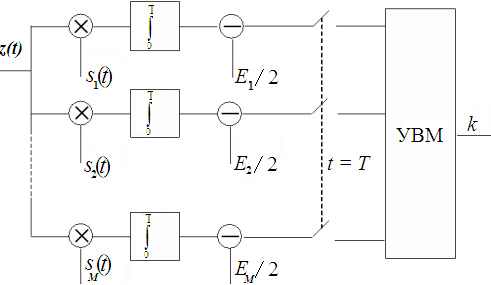
Рис. 17.3. Структура приемника максимального правдоподобия
Пример. В проводных системах связи с амплитудной телеграфией могут применяться посылки в форме прямоугольного видеоимпульса. Предположим, что сигнал, соответствующий символу «1», представляет собой прямоугольный видеоимпульс с амплитудой a и длительностью T. Тогда корреляционный интеграл имеет вид
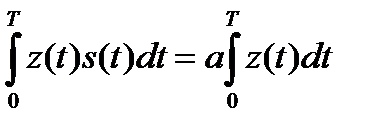 ,
,
порог равен Е/2 = а2Т/2, тогда решающее правило имеет вид
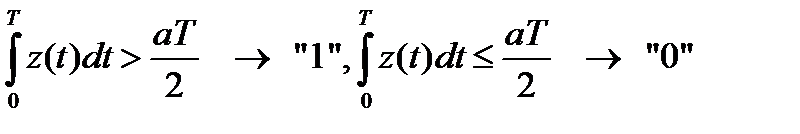 .
.
Структурная схема приемника показана на рисунке 17.4. Постоянная времени интегрирующей цепи должна быть много больше длительности посылки T. В этом случае начальный участок экспоненты a(1- e-t/(RC)), отображающей заряд емкости, можно аппроксимировать прямой линией с тангенсом угла наклона a/(RC), равным производной экспоненты в нуле. Тогда за время T напряжение на входе решающего устройства, обусловленное сигналом, составит aT/(RC), а значение порога должно быть равно aT/(2RC).
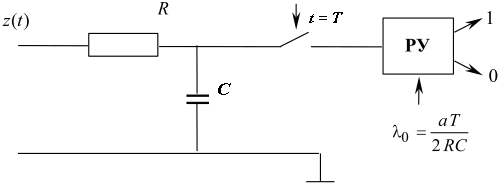
Рис. 17.4. Структурная схема приемника прямоугольного видеоимпульса
Пример. Предположим, что в двоичной системе связи с амплитудной телеграфией сигнал, соответствующий символу «1», представляет собой прямоугольный радиоимпульс с амплитудой a и длительностью T. Тогда s(t) = cos(ω0t + φ), корреляционный интеграл имеет вид
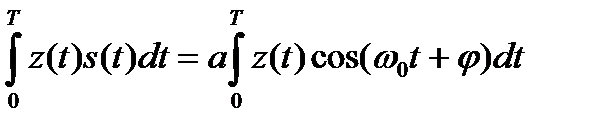 ,
,
а порог равен Е/2 = а2Т/4. Сокращая на a и применяя реальный интегратор в виде RC -цепи, получаем структуру приемника, показанную на рисунке 17.5.
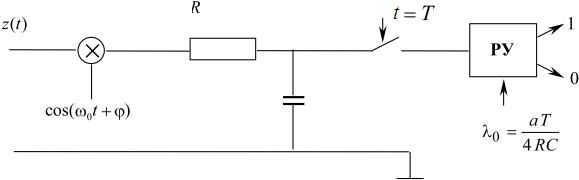
Рис. 17.5. Структурная схема приемника прямоугольного радиоимпульса
Пример. В двоичной системе связи с фазовой телеграфией сигналы s1(t) и s2(t), соответствующие символам «1» и «0», являются противоположными
s1(t) = cos(ω0t + φ); s2(t) = cos(ω0t + φ + π) = -s1(t)
Принятие решения основано на сравнении величин
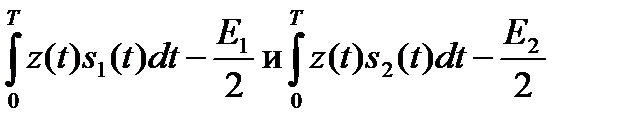 .
.
C учётом равенства энергий правило принятия решения упрощается и принимает вид
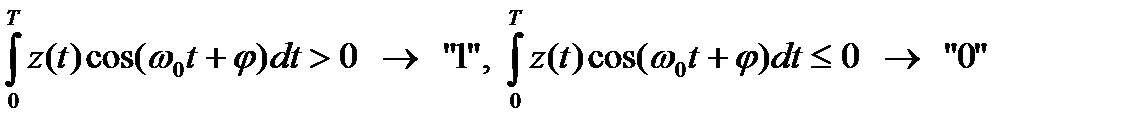 .
.
Дата добавления: 2017-10-04; просмотров: 1946;











