Модели дискретных каналов

Дискретными называются каналы, входные и выходные сигналы которых принимают конечное число мгновенных значений. Понятие дискретного канала естественно возникает при передаче дискретных сообщений и определяется как совокупность технических средств, включенных между кодером и декодером канала (рис. 14.1).

Переход от дискретных сигналов к непрерывным осуществляется на передающей стороне при манипуляции параметрами непрерывной несущей. На приемной стороне дискретные сигналы появляются на выходе первой решающей схемы (демодулятора).

Свойства дискретного канала определяются непрерывным каналом и структурой модема. Дискретный канал задается множеством входных {s_i}, 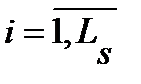и выходных {y_j}, 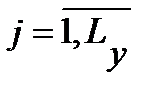символов (сигналов), длительностью символов τ и условными вероятностями P(y_j/s_i) преобразования входных символов в выходные. Обычно длительности всех входных и выходных символов одинаковы. Объемы алфавитов входных L_s и выходных L_y сигналов в общем случае могут быть разными, причем L_y ≥ L_s. Однако в большинстве случаев L_y = L_s. Для дискретных каналов широко используется представление принятой последовательности символов Y = (y₁, y₂,..., y_n) в виде суммы переданной последовательности S = (s₁, s₂,..., s_n) и комбинации помехи (вектора ошибки) E = (e₁, e₂,..., e_n)

,

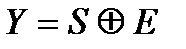где – понимается как поразрядное сложение S и E по модулю L_s. В случае двоичных последовательностей (L_s = 2) нулевой символ вектора ошибки e_i = 0 означает, что i-й символ принят правильно (y_i = s_i), а e_i = 1 указывает на ошибку в приёме (y_i ≠ s_i).

Классификацию дискретных каналов удобно вести по вектору ошибки Е. Разные модели каналов различаются распределением вероятностей вектора Е. Наиболее распространены следующие модели [2].

Канал без памяти – это канал, в котором символы e_i являются независимыми СВ. Прием каждого сигнального символа в таком канале не зависит от результата приема предыдущих символов. При наличии такой зависимости имеет место канал с памятью. Дискретный канал называется стационарным, если вероятность ошибочного приема символов не изменяется с течением времени.

В силу простоты технической реализации наибольшее применение находят каналы, сигналы в которых представляются двоичным кодом.
Такие каналы называются двоичными (бинарными) и задаются с помощью графа (рис. 14.2). Вероятности P(0/0) и P(1/1) характеризуют правильный прием символов 0 и 1 соответственно, a P(1/0) и P(0/1) – вероятности ошибок при приеме символов 0 и 1.

Симметричным двоичным называется канал, в котором вероятности ошибок при приеме 0 и 1 одинаковы, P(1/0) = P(0/1), а следовательно, равны и вероятности правильного приема символов P(0/0) = P(1/1) = 1 - p. Для симметричного стационарного канала без памяти вероятность искажения i-го символа P(e_i = 1) = p, а вероятность правильного приема P(e_i = 0) = 1 – p.

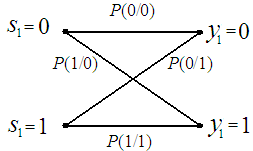
Рис. 14.2. Граф двоичного канала

Двоичный канал без памяти со стиранием отличается от рассмотренного тем, что выходной алфавит помимо 0 и 1 содержит третий символ «?» – символ стирания. Он появляется в тех случаях, когда демодулятор не может надежно опознать переданный символ. Такой канал часто используется в системах передачи информации с обратной связью, когда при приеме символа «?» производится повторение передачи. Это позволяет значительно снизить вероятность ошибочного приема за счет уменьшения скорости передачи.

Марковский канал является простейшей моделью дискретного канала с памятью. Он характеризуется вектором ошибки, символы которого образуют простую цепь Маркова [12]. Вероятность искажения символа в этом канале зависит от результата приема только предыдущего символа.

Марковская модель задается матрицей переходных вероятностей:

,

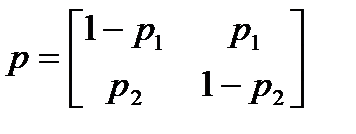где p₁ – условная вероятность принять (i + 1)-й символ ошибочно, если i-й принят правильно; 1- p₁ – условная вероятность принять (i + 1)-й символ правильно, если i-й принят правильно; p₂ – условная вероятность принять (i + 1)-й символ ошибочно, если i-й принят ошибочно; 1- p₂ – условная вероятность принять (i + 1)-й символ правильно, если i-й принят ошибочно.

Безусловная (средняя) вероятность ошибки в рассматриваемом канале должна удовлетворять уравнению:

p(x_i+1 / x_i) = p₂ ∙ p_ош(x_i) + p₁ ∙ p_прав(x_i)

или

p(x_i+1 / x_i) = p₁ / (1 + p₁ + p₂).

Данная модель имеет достоинство – простоту использования, но не всегда адекватно воспроизводит свойства реальных каналов. Большую точность позволяет получить модель Гильберта для дискретного канала с памятью. В такой модели канал может находиться в двух состояниях S₁ и S₂. В состоянии S₁ ошибок не происходит; в состоянии S₂ ошибки возникают с вероятностью p₂.

Также считаются известными вероятности перехода p(S₁ / S₂) из состояния S₁ в S₂ и вероятности перехода p(S₂ / S₁) из состояния S₂ в состояние S₁. В этом случае простую марковскую цепь образует не последовательность ошибок, а последовательность переходов:

,

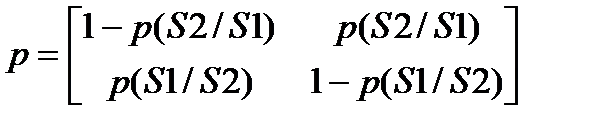При этом достаточно легко выразить безусловные вероятности нахождения канала в состояниях S₁ и S₂:

, ,

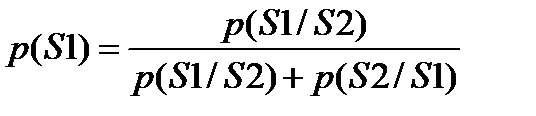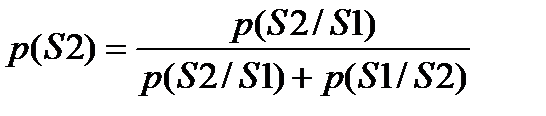Безусловная вероятность ошибки в этом случае может быть определена по формуле:

.

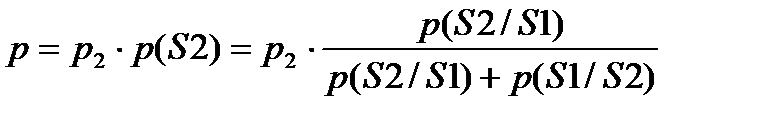Наиболее часто при использовании модели Гильберта для двоичного канала полагают p₂ = 1/2, т.е. состояние S₂ рассматривается как полный обрыв связи. Это согласуется с представлением о канале, в котором действуют коммутационные помехи.

Из других моделей симметричных двоичных каналов следует отметить канал с пакетами ошибок, который характеризуется тем, что искажающие символы (единицы) вектора ошибки группируются в пакеты. Такое группирование происходит, если в непрерывном канале, входящем в дискретный, действуют сильные замирания сигналов на время длительности нескольких символов или присутствуют импульсные помехи большой длительности. Подобные каналы задаются вероятностями искажений серий из q символов подряд.