Количество информации, переданной по непрерывному каналу

Вместо последовательностей символов для дискретного канала, в непрерывном канале осуществляется передача последовательности непрерывных величин с дискретным или непрерывным временем (в первом случае эти последовательности можно представить в виде импульсов различной величины, появляющихся в определенные моменты времени, а во втором случае как непрерывные функции времени).

Количество передаваемой информации:

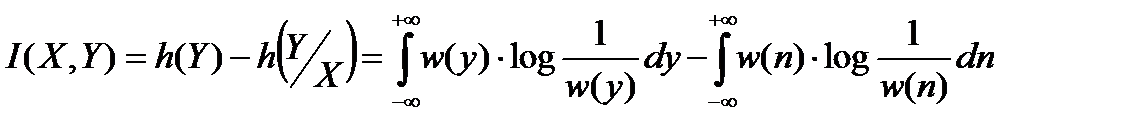, (15.6)

где w(y) – плотность распределения вероятности выходных случайных величин;

w(n) – плотность распределения вероятности помехи (аддитивной);

h(Y) – дифференциальная энтропия сигнала y;

h(Y/X) – условная дифференциальная энтропия сигнала y при известном сигнале x;

Отметим следующие свойства количества информации, передаваемой в непрерывном канале:

I(Y,X) ≥ 0, причём I(Y,X) = 0 тогда, и только тогда, когда вход и выход канала статистически независимы, т.е. w(y / х) = w(y);

I(Y,X) = I(X,Y) – свойство симметрии;

I(Y,X) = ∞, если помехи в канале отсутствуют, т.е. y = x, n = 0

Дифференциальная энтропия h(Y) уже не представляет собой среднее количество информации, выдаваемое источником сигнала (для непрерывного сигнала оно бесконечно). Аналогично h(Y/X) не представляет собой количество информации, потерянной в канале, поскольку эта величина тоже бесконечна. Поэтому дифференциальную энтропию следует понимать лишь формально, как некоторую вспомогательную величину полезную при расчетах.

Если помеха аддитивная y = x + n , то нетрудно показать, что

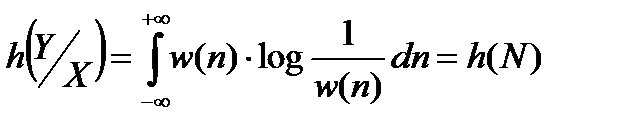, (15.7)

где w(n) – плотность распределения вероятности помехи, а h(N) – дифференциальная энтропия помехи.

Выражение для определения количества информации, переданной по непрерывному гауссовскому каналу (нормальный закон распределения вероятностей сигнала и помехи):

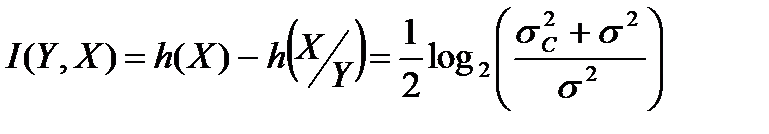. (15.8)

где

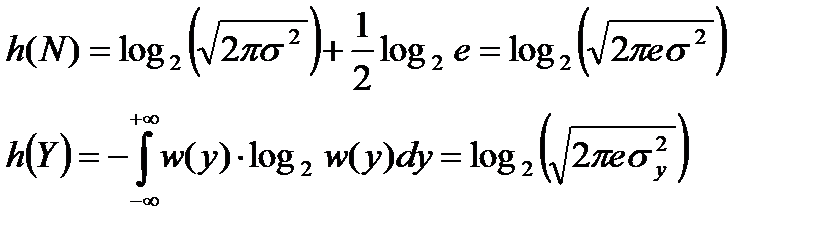(15.9)

Полученное выражение показывает, что пропускная способность гауссовского канала с дискретным временем определяется отношением дисперсии сигнала σ_с² к дисперсии помехи σ². Нередко величину σ_с² / σ² = h² называют отношением сигнал/шум. Чем больше это отношение, тем выше пропускная способность.