Пропускная способность симметричного дискретного канала без памяти

Пропускная способность дискретного канала с учетом (15.2), по которому передается m дискретных сигналов, вычисляется по формуле

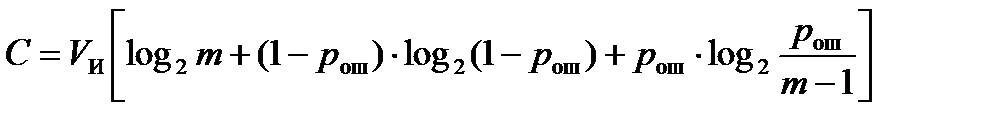, 15.3)

где V_И= 1/T – скорость модуляции, бод; T – длительность сигнала; p_ош– вероятность ошибки в канале. Заметим, что пропускная способность дискретного канала без помех (при p_ош = 0): C_ДК= V_И [log₂m].

В частности пропускная способность двоичного канала (m = 2):

C_ДК = V_И [1 + (1- p_ош) log₂(1- p_ош) + p_ош log₂(p_ош)]. (15.4)

Зависимость отношения C/V_И от вероятности ошибки p_ош, рассчитанная по формуле (15.4), показана на рис. 15.1.

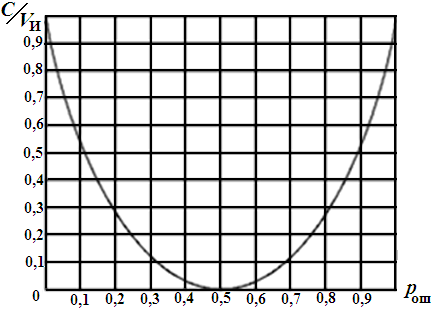
Рис. 15.1. Пропускная способность дискретного канала

Как следует из графика, при p_ош= 0,5 пропускная способность двоичного канала равна нулю (С = 0). Этот случай называют обрывом канала. Действительно вероятность ошибки p_ош= 0,5 можно получить и без передачи информации по каналу связи. А при p_ош= 1 пропускная способность такая же, как и при p_ош= 0 (канал без помех). Это объясняется тем, что при p_ош = 1 достаточно заменить нули на единицы и единицы на нули, чтобы абсолютно правильно восстановить переданный сигнал.

Пример.Определим пропускную способность двоичного телеграфного канала, если скорость передачи в нем 1000 бит/с и вероятность ошибки 10^-3 и сделаем вывод о том насколько отличается пропускная способность этого канала от идеального. Согласно формуле (15.4), при заданных параметрах:

C_ДК= 1000 [1 + 0,001 · log₂0,001 + (1-0,001) · log₂(1-0,001)] = 989 [бит/с].

Для идеального канала при p_ош = 0 получаем C_ДК= V_И= 1000бит/с. Сравнение этих величин показывает, что ошибки в канале привели к уменьшению пропускной способности на 11 бит/с (т.е. потери составили 1,1%).