Кинематика вращательного движения материальной точки

При описании вращательного движения интересуются обычно не длиной пути и величинами линейной скорости и ускорения, а величинами углов поворота, угловой скорости (или частоты вращения), углового ускорения.

Для определения положения в пространстве вращающегося тела задают положение оси вращения, а величину угла поворота j обозначают «псевдовектором», направленным вдоль оси вращения по «правилу буравчика» – правого винта (рис.1.7)

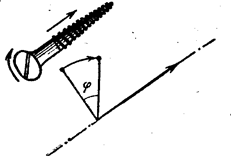
Рисунок 1.7 К определению угла поворота

Для количественной характеристики быстроты вращения введена величина мгновенной угловой скорости 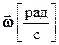или [c^-1]. Абсолютное значение вектора 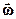равно производной по времени от угла поворота

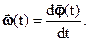
Средняя угловая скорость за время Dt равна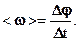

Очевидно, что векторы 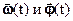по направлению совпадают (рис. 1.8).

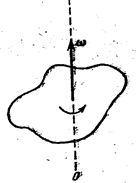
Рисунок 1.8 К определению направления вектора угловой скорости

При неравномерном вращении используется векторная величина углового ускорения 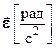или [c^-2], по величине равная

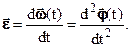
Угловая скорость при равнопеременном вращении можно найти из выражения, очень похожего для формулы прямолинейного равнопеременного движения

w_t = w₀ ± et.

Среднюю угловую скорость при равнопеременном вращении можно найти из выражения, аналогичного выражению средней скорости при прямолинейном равнопеременном движении:

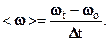
Таким образом, каноническое уравнение движения при вращении может быть представлено в виде:

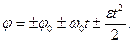
Угловой путь j [рад] может быть найден из выражений, «симметричных» полученным при описании прямолинейного движения:

– Dj = w×Dt - равномерное вращение (w =const, e = 0);

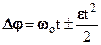– - равнопеременное вращение (w = w_о±et, e = const);

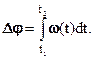– - неравномерное вращение (w = w(t) – функция, описывающая зависимость угловой скорости от времени.

Применение единицы СИ «радиан» далеко не всегда удобно при описании вращения. Широко применяются понятия частоты n 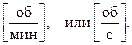Используются соотношения, связывающие w и n, j и N– число оборотов, совершенное точкой (телом):

w = 2pn, j = 2pN.