Геометрическое подобие

Рассмотрим геометрическое подобие. Пусть имеются два тела 1 и 2 с центрами тяжести О₁ и О₂ (рис. 2.1. а, б). Если поместить тело 2 внутри тела 1 так, чтобы центры тяжести их совпали, а затем тело 1 деформировать и вращать до тех пор пока, в результате равномерной деформации тела 1 все точки контура или границы обоих тел совпадут, то такие тела подобны. Такое расположение тел 1 и 2 называется сходственным расположением. Одновременные координатные оси О₁х₁ и О₂х₂; О₁у₁и О₂у₂, О₁z₁ и О₂z₂ также совпадут между собой, и

будут называться сходственными.

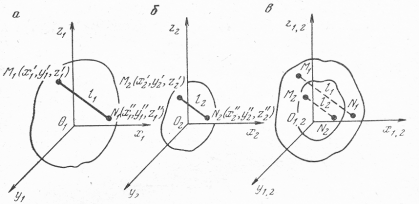
Рис. 2.1. Определение геометрического подобия:

а – тело; б – тело; в – совмещение тел 1 и 2

Нетрудно видеть, что при подобных телах 1 и 2 для любой точки в теле 1 может быть найдена сходственная точка в теле 2.

Проведем в телах 1 и 2 через две произвольные точки М₁N₁ отрезок l₁, М₂N₂ – l₂. Следовательно, отрезки l₁ и l₂ в результате равномерной деформации совпадут (рис. 2.1. в), т.е. l₁ и l₂ – сходственные линейные размеры, или сходственные параметры подобных тел. Очевидно, что в подобных телах сходственные криволинейные отрезки, а также замкнутые кривые могут быть совмещены в результате равномерной деформации. Примерами сходственных размеров могут явиться диаметры d₁ и d₂, высоты h₁ и h₂ двух подобных цилиндров и т.д.

Так как при равномерной деформации все размеры тела изменяются в одинаковое число раз, то для двух подобных тел должно выполняться соотношение

,

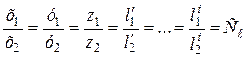(2.1)

где	х1,у1,z1	–	координаты тела 1;
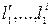
		–	параметры тела 1;
	х2,у2,z2	–	координаты тела 2 (сходственные);
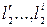
		–	сходственные параметры тела 2;
	Сl	–	множитель подобия, показывающий во сколько раз нужно изменить размеры одного тела, чтобы оба тела совпали.

При моделировании физических процессов большие удобства дает переход на безразмерные зависимости между параметрами.

Выразив все члены равенства (2.1) через один из сходственных членов, например, через параметр 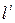, и обозначив

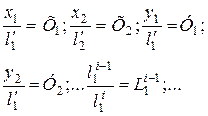(2.2)

получим

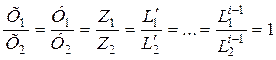(2.3)

откуда

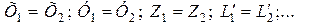и т.д. (2.4)

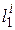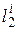При этом X, У, Z являются безразмерными величинами, выраженными в долях сходственных параметров и , которые выбраны произвольно в качестве единиц измерения или масштаба длин.

Таким образом, равенства (2.3) и (2.4) выражают весьма существенное свойство геометрически подобных систем: если в качестве масштабов для измерения длин выбрать сходственные параметры подобных систем, то у них (систем) безразмерные координаты сходственных точек, а также безразмерные сходственные параметры соответственно равны.

Соотношения, полученные из выражения (2.2)

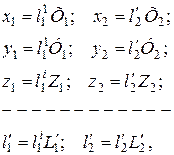(2.5)

называются масштабными преобразованиями, причем .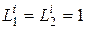

Пользуясь изложенными сведениями о геометрическом подобии, можно доказать основное свойство геометрически подобных систем: если в качестве масштабов выбрать сходственные параметры, то уравнения, описывающие подобные геометрические системы, после приведения их (с помощью масштабных преобразований) к безразмерному виду станут тождественно одинаковы.

Выше были рассмотрены подобные системы. Однако возможны случаи, когда совмещение двух геометрических систем может быть осуществлено только путем неравномерной деформации (неодинаковой для всех направлений). Такие системы называют аффинными.

Две системы аффинны, если для каждой точки А₁ системы 1 с координатами x₁, y₁, z₁ может быть найдена точка А₂ с координатами x₂, y₂, z₂, чтобы удовлетворялись соотношения:

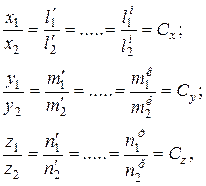(2.6)

где l, m, n – параметры;

C_х, C_у, C_z – множители аффинности.

Точки А₁ и А₂ являются сходственными точками аффинных систем, или аффинно-сходственными точками. Параметры l₁ и l₂ , m₁ и m₂ , n₁ и n₂ являются сходственными точками аффинных систем или аффинно-сходственными параметрами. Параметры 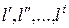называются соответственными оси х;

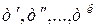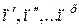и соответственными осями у и z.

Для аффинных систем справедливо следующее положение: если отношения сходных масштабов координатных осей х_0,1 и х_0,2 ; у_0,1 и у_0,2 ; z_0,1 и z_0,2 равны отношениям соответственным этим осям сходственных параметров, т.е.:

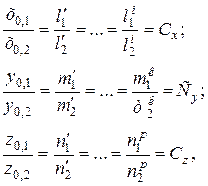(2.7)

то функции или уравнения, которые описывают аффинные системы, после приведения с помощью аффинно-масштабных преобразований к безразмерному виду становятся тождественно одинаковыми.

Докажем это положение. Для этого возьмем две аффинные системы, описывающие в общем случае следующими уравнениями

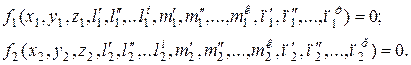(2.8)

Координаты и параметры уравнения (2.8) удовлетворяют равенствам (2.6).

Для приведения уравнений (8) к безразмерному виду введем аффинно-масштабные преобразования:

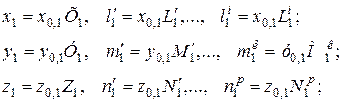(2.9)

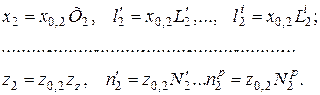(2.10)

Масштабы координатных осей x_0,1 и x_0,2; y_0,1 и y_0,2; z_0,1 и z_0,2 в уравнениях (2.9) и (2.10) удовлетворяют равенствам (2.7).

Подставив масштабные преобразования (2.9) и (2.10) в равенство (2.6), получим

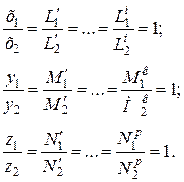(2.11)

Как видно из соотношений (2.11), безразмерные координаты аффинно-сходственных точек и аффинно-сходственные безразмерные параметры аффинных систем соответственно равны.

Существенное отличие этого вывода от аналогичного вывода, полученного для подобных систем, заключается в том, что все безразмерные коэффициенты и параметры систем выражены в долях одного и того же масштаба. Безразмерные же координаты и соответственные им параметры аффинных систем выражены в долях различных масштабов.

Подставляя преобразования (2.9) и (2.10) в уравнение (2.8) получим

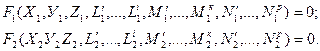(2.12)

Из (2.11) следует, что

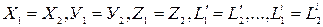(2.13)

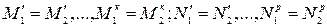(2.14)

Учитывая, что равенства (2.13) сохраняют свою силу для любой пары сходственных точек (т.е. при любых Х, У, Z), то функции F₁ и F₂ тождественно равны

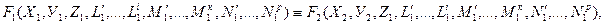
что и требовалось доказать.

Рассмотрим примеры.

Пример 1. Два подобных эллипсоида, у которых начало координат взято в

центре, а направления координатных осей и главных осей эллипсоида совпадают, описываются уравнениями.

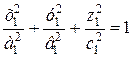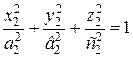и , (а)

где 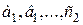– главные оси эллипсоида.

Так как эллипсоиды подобны, то в сходственных точках должно быть

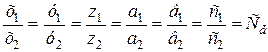. (б)

Составим безразмерные уравнения эллипсоидов. Для этого примем за масштабы главные полуоси а₁ и а₂. Тогда масштабные преобразования

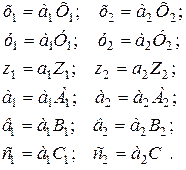(в)

Вводя масштабные преобразования в уравнения эллипсоидов (а), получим

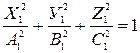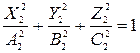и (г)

Из условий (в) имеем

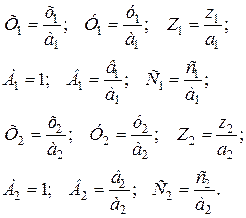
Из условия (б) следует

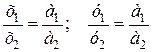и т.д.,

то

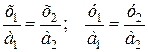и т.д.

или

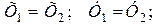и т.д.

Следовательно, уравнения эллипсоидов можно записать в виде одного безразмерного уравнения

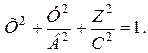
причем А₁= А₂ = 1.

Пример 2. Те же эллипсоиды, если их безразмерные полуоси не равны
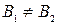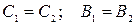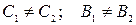при при при 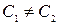, но для подобных эллипсоидов имеет место равенство отношений одноименных полуосей

,

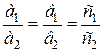а для аффинных

.

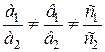Покажем, что совмещение аффинных эллипсоидов возможно осуществить путем неравномерной деформации.

Введем аффинные масштабные преобразования, в которых масштабы в разных направлениях различны.

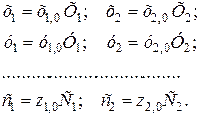
Подставив их в уравнения эллипсоидов, получим

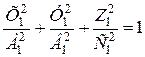и .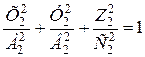

Для того чтобы эти уравнения были тождественны, необходимо соблюдение условий

А₁=А₂; В₁=В₂; С₁=С₂; Х₁=Х₂ и т.д.

или

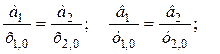и т.д.,

откуда получим

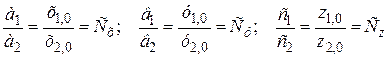(а)

Тогда имеем одно уравнение эллипсоида в безразмерном виде

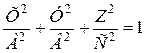. (б)

Следовательно, с помощью аффинных масштабных преобразований, удовлетворяющих условию (а), уравнения эллипсоидов сведены к единому безразмерному уравнению (б), которое является тождественно одинаковым для всех подобных эллипсоидов.

Следует иметь ввиду, что масштабные преобразования являются частным случаем аффинно-масштабных преобразований, когда масштабы различных осей равны друг другу, т.е. 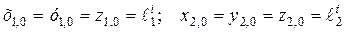. В соответствии со сказанным можно представить, что уравнение

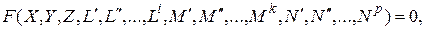
где F – функция определенного вида при одинаковых масштабах координатных осей, т.е. при х₀=у₀=z₀ описывает целый класс геометрических подобных систем. Если в двух системах имеет место неравенство хотя бы двух из одноименных безразмерных параметров (например, ( 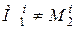), то такие системы будут не подобными, а аффинными.

Приведенные выше свойства подобных и аффинных геометрических систем будут использованы в дальнейшем при рассмотрении подобия физических полей, которые являются формальным аналогом геометрической аффинности.