Геометрическое и физическое подобие
При физическом моделировании рассматривают классы однородных явлений, имеющих одинаковую физическую природу, например, класс явлений, связанный с изучением теплопроводности. Из класса однородных явлений выделяют группу подобных между собой явлений.
Принцип выделения группы подобных явлений можно рассмотреть на простейшем примере геометрического подобия однородных фигур (прямоугольников, треугольников и т.п.). Подобные однородные фигуры отличаются только масштабом. Любая из подобных фигур может быть получена из другой фигуры той же группы путем умножения ее линейных размеров на постоянный масштабный множитель Сl . Этот множитель называется константой подобия или множителем подобного преобразования. Так, для подобных треугольников А1В1С1 и А2В2С2 его стороны соотносятся следующим образом: А1В1= Сl· А2В2; В1С1= Сl· В2 С2; С1 А1= Сl· С2А2 . Причем для каждой пары фигур Сl=const.
В применении к технологическим процессам понятие геометрического подобия расширяется и распространяется на все физические величины, характеризующие данный процесс. Два подобных процесса отличаются масштабом физических величин, поэтому для каждой из этих величин (плотности ρ, вязкости μ, скорости w, силы f и т.п.) имеется свой множитель подобного преобразования ( 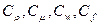 и др.).
и др.).
Физические составляющие одного из процессов (ρ1, μ1, w1, f1 и др.) выражаются через параметры второго процесса (ρ2, μ2, w2, f2 и др.) при помощи соответствующих множителей, которые не равны друг другу ( 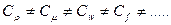 ):
): 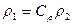 ;
; 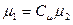 ;
; 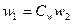 ;
; 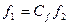 и т.д.
и т.д.
Физические величины по мере протекания процесса изменяются во времени и в пространстве - объеме аппарата, возникают поля величин – температур, давлений, скоростей, концентраций. Существует понятие о временном подобии и подобии полей физических величин.
Временное подобие – это подобие отрезков времени, отсчитываемых от начала процесса.
Подобие полей физических величин заключается в постоянном соотношении физических величин процессов для любых двух сходственных точек рассматриваемых аппаратов. Подобные поля физических величин могут наблюдаться только в геометрически подобных аппаратах. Поэтому необходимой предпосылкой физического подобия процессов является геометрическое подобие аппаратов.
Физические явления считаются подобными при условии подобия всех величин, характеризующих эти явления. Физическое подобие наступает, если в геометрически подобных системах подобны поля всех физических величин в подобные (сходственные) моменты времени от начала процесса.
Любой процесс отличается от подобного ему процесса той же группы только масштабом характерных величин, отражающих различные стороны процесса. Все процессы данной группы представляют собой один и тот же процесс в разных масштабах. Следовательно, для того, чтобы судить обо всей группе процессов, достаточно изучить один из подобных процессов данной группы. Для изучения необходимо выбрать удобный масштаб и воспроизвести процесс в малой модели. И затем по результатам опытов можно судить о подобном процессе, протекающем в большом масштабе промышленного аппарата.
Выбор множителей подобного преобразования для каждой из физических величин не произволен. Значения констант подобия для различных физических величин определяется особым правилом, вытекающим из основных теорем подобия. Используются три основные теоремы, которые отвечают на практические вопросы, возникающие при постановке модельных или натурных опытов:
- какие величины нужно определять в опытах;
- в какой форме следует представлять количественные результаты опытов;
- на какие промышленные аппараты можно распространить результаты модельных опытов.
Первая теорема подобия, известная как теорема подобия Ньютона, отвечает на первый вопрос и формулируется таким образом: подобные между собой явления имеют одинаковые критерии подобия.
Рассмотрим справедливость формулировки на следующем примере. Пусть в подобных системах происходит подобное движение тел. Основным физическим законом для движения тел является второй закон Ньютона:
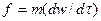 .
.
Для двух подобных систем уравнения имеют вид:
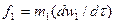 ;
; 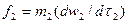 .
.
Физические величины, характеризующие поведение двух систем, отличаются только масштабом, поэтому
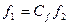 ;
; 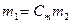 ;
; 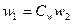 ;
; 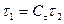 ;
; 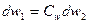 ;
; 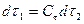 .
.
Разделим исходные уравнения двух систем одно на другое:
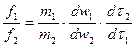 или
или 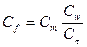 . (1.1)
. (1.1)
Следовательно, при подобии двух систем
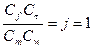 .
.
Комплекс множителей подобного преобразования 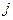 называется индикатором подобия. Для двух заведомо подобных явлений он равен единице.
называется индикатором подобия. Для двух заведомо подобных явлений он равен единице.
Отсюда следует вторая формулировка первой теоремы подобия, предложенная М.В. Кирпичевым: у подобных явлений индикаторы подобия равны единице.
Из уравнения (1.1) следует, что
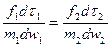 и
и 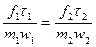 .
.
Таким образом, для двух и ряда подобных явлений (т.е. группы подобных явлений данного класса) сохраняется численное равенство величин 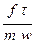 , что записывается так:
, что записывается так: 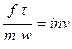 (инвариантно, неизменно) или
(инвариантно, неизменно) или 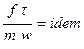 (одно и то же).
(одно и то же).
В честь Ньютона безразмерный комплекс физических величин назван числом Ньютона: 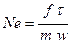 .
.
Следовательно, для ряда (группы) подобных процессов, класс которых описывается исходным физическим уравнением второго закона Ньютона, справедливо равенство
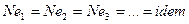 .
.
В частности, если рассматривать подобные процессы движения в модели и реальном объекте, то
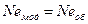 .
.
Это равенство является математической формулировкой первой теоремы по числу Ньютона. Число Ньютона представляет собой критерий подобия, т.к. равенство этих комплексов для ряда подобных процессов является признаком (критерием) их подобия.
Первая теорема подобия показывает, что в правильно поставленных опытах целесообразно измерять только те физические величины, которые входят в критерии подобия исследуемого процесса.
Критерии подобия могут быть получены из уравнений, описывающих исходный процесс. При этом безразлично, записаны они в алгебраической или дифференциальной форме.
Наиболее важными свойствами критериев подобия является следующие. Они безразмерны, но имеют определенный физический смысл. Так критерий Ньютона представляет собой меру отношения импульса силы 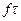 и количества движения
и количества движения 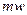 и выражает соотношения активных и противодействующих сил. В частных случаях движения в зависимости от конкретных выражений для силы, массы и скорости (как это будет показано ниже) критерий
и выражает соотношения активных и противодействующих сил. В частных случаях движения в зависимости от конкретных выражений для силы, массы и скорости (как это будет показано ниже) критерий 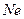 принимает иной вид, преобразуясь в критерий Рейнольдса, Эйлера, Фруда, Галилея и др.
принимает иной вид, преобразуясь в критерий Рейнольдса, Эйлера, Фруда, Галилея и др.
Определенный физический смысл каждого критерия подобия отличает его от произвольно подобранных безразмерных комплексов из случайных физических величин.
Вторая теорема подобия – теорема Федермана – Бекингема – отвечает на второй вопрос: как обрабатывать результаты опытов. Согласно этой теореме, решение любого дифференциального уравнения, связывающего между собой влияющие на процесс переменные, может быть представлено в виде зависимости между безразмерными комплексами этих величин, т.е. между критериями подобия.
Критерий подобия 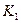 , содержащий интересующую нас величину, должен быть выражен как функция других критериев, К2, К3, К4, …, отражающих различные стороны процесса:
, содержащий интересующую нас величину, должен быть выражен как функция других критериев, К2, К3, К4, …, отражающих различные стороны процесса:
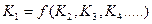 . (1.2)
. (1.2)
В общем случае вид этой функции заранее неизвестен и определяется при обработке экспериментальных данных. Результаты опытов при их обработке наиболее целесообразно представлять, например, в виде степенной зависимости
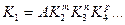 , (1.3)
, (1.3)
где 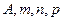 - постоянные коэффициенты, найденные из опытов.
- постоянные коэффициенты, найденные из опытов.
Замечательной и важной в практическом отношении особенностью метода подобия является то, что исходная система дифференциальных физических уравнений не решается аналитически, а используется для определения вида и числа критериев в функции (1.2). Практическое, экспериментальное решение исходной системы достигается в форме (1.3).
Каждое критериальное уравнение, несмотря на эмпирический способ его получения в явной форме, имеет определенный физический смысл, потому что оно является уравнением подобия и отражением законов природы, выраженных исходной системой физических уравнений.
Каждый из критериев обобщенного уравнения отражает какую-либо одну из основных сторон процесса, а все критериальное уравнение – весь процесс в целом.
Все безразмерные величины, получаемые при подобном преобразовании дифференциальных уравнений, представляют собой, как уже было отмечено, критерии подобия. Различают критерии-комплексы, составленные из разнородных физических величин (подобно критерию Ньютона), и критерии-симплексы или параметрические, масштабные критерии, составленные из одноименных величин (например, 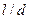 - относительная длина трубы с длиной
- относительная длина трубы с длиной 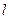 и диаметром
и диаметром 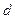 ).
).
Из одних и тех же физических величин можно составить различные критерии подобия. Их можно делить, умножать, получая новые критерии подобия с иным физическим смыслом. Поэтому решение уравнения в форме (1.3) не является единственным. Например, если для двух разных критериев показатели степени одинаковы, то наиболее целесообразно эти критерии объединять в один. В этой связи один и тот же процесс может быть описан несколькими системами, составленными из критериев. Так, для процессов кипения жидкостей существует более десяти обобщенных зависимостей, основанных на практически совпадающих экспериментальных данных.
Третья теорема подобия, или теорема М.В. Кирпичева и А.А. Гухмана, формулирует необходимые и достаточные условия подобия явлений: явления между собой подобны, если они описываются одной и той же системой дифференциальных уравнений и имеют подобные условия однозначности.
Подобию же условий однозначности при идентичности дифференциальных уравнений, описывающих процессы, отвечает равенство определяемых критериев. Таким образом, третью теорему подобия можно сформулировать и так: явления подобны, если их определяемые критерии численно равны.
Следствием равенства определяющих критериев является равенство определяемых критериев для натуры и модели. Поэтому зависимость типа уравнения (1.3), полученная обобщением результатов опытов на модельной установке, будет справедлива в пределах изменения определяющих критериев для всех подобных процессов, в том числе и для натуры.
Моделирование процессов и аппаратов осуществляют обычно в таком порядке:
1) составляют математическое описание процесса в виде уравнений, описывающих процесс, и условий однозначности;
2) выводят критерии подобия и из них выделяют критерий, содержащий искомую величину. Этот критерий (определяемый) выражается в неявной функции от остальных критериев, называемых определяющими;
3) из условий равенства критериев в модели и образце выбирают константы подобия для каждой из физических величин;
4) на основе этих данных рассчитывают и изготавливают модель, рабочий объем которой геометрически подобен рабочему объему промышленного аппарата. Масштаб модели определяют с учетом размеров и производительности аппарата, обеспечивая требуемые скорости, расходы, температуры и другие величины для рабочих тел;
5) принимают меры для того, чтобы при проведении опытов определяющие критерии в модели изменялись в тех же пределах, что и в промышленном аппарате.
При выполнении указанных требований все соответственные величины для модели и образца, характеризующие явление, будут пропорциональны между собой, при этом подобие натуре наступит по всему объему модели.
Дата добавления: 2016-06-29; просмотров: 4639;











