ОБЩИЕ СВЕДЕНИЯ О ГЕОМЕХАНИЧЕСКИХ ПРОЦЕССАХ И МЕТОДАХ ИХ ИССЛЕДОВАНИЙ
Моделирование как метод научного исследования получило развитие в середине девятнадцатого столетия. До этого ряд ученых на основе интуитивных соображений зачастую обращались при решении отдельных задач, в основном, строительных и архитектурных. Познавательные возможности таких моделей были довольно ограниченными, на что обратили свое внимание еще ученые средневековья Леонардо да Винчи и Галилео Галилей.
В Х1Х в. начинается период от спорадического применения моделей, при котором исследователь руководствовался лишь собственным чутьем и весьма непосредственными соображениями, обобщающие его собственный по необходимости ограниченный опыт, к систематическому применению моделирования, оказавшемуся возможным и плодотворным благодаря активизирующейся в это время разработке теоретических основ моделирования. С помощью моделей начинается изучение все более глубоких связей и отношений объективного мира. Успехи на этом пути привели к постепенному превращению моделирования из полуэмпирического способа исследований, которым пользовались некоторые ученые при решении частных задач, в метод научного исследования, широко используемый в физике, химии, технических и других науках. Были разработаны положения теории подобия, которые явились основой применения моделей в таких областях науки, как теплотехника, гидродинамика, строительная механика, гидродинамика, строительная механика, физика твердого тела и др.
Разработка математически точной теории подобия способствовала внедрению в научное мышление этого стиля исследований, который широко распространен в современной науке и который предполагает смелое, инициативное, но в то же время научно обоснованное использование одной, более развитой отрасли науки для решения задач другой; и в это же время применение теории подобия требовало более высокого уровня развития абстрактного мышления и наличия значительного количества фактов из различных областей науки.
Как блестящий образец использования моделирования, следует отметить разработку гениальным механиком-самоучкой И.П.Кулибиным проекта однопролетного арочного моста через р. Нева в Петербурге в конце XVIII в. Мост длиной 300 м должен был быть выполнен из дерева. Изобретатель построил модель моста 1/10 натурных его размеров и испытал ее под нагрузкой в 3870 пудов (61,92 т.) в течение 28 дней, при этом в модели не обнаружилось никаких изменений. Модель Кулибина просуществовала более 30 лет, выполняя в последствии роль одного из мостов Таврического сада. Важно отметить, что Кулибин при испытании своей модели правильно решил задачу о редуцировании нагрузки в соответствии с линейным масштабом модели и с учетом реологических свойств древесины.
Во второй половине Х1Х в. началось интенсивное применение моделей в различных областях физики. К этому времени законы механики были достаточно хорошо изучены и для большинства физиков объяснять явление значило построить его механическую модель.
Именно так поступил Дж. К. Максвелл, сформулировав важнейшие законы электродинамики на основе своих электромеханических аналогий. Модели Максвелла явились одними из первых в длинном ряду теоретических моделей, которым предстояло сыграть выдающуюся роль в развитии физики и других областей научного значения. В частности, электромеханические аналогии могут быть использованы как мощный инструмент при решении сложных задач петромеханики.
В качестве моделей используются довольно крупные и сложные объективно существующие устройства, природные объекты, знаковые системы постоянно возрастающей сложности разнообразные объекты, существующие лишь в сознании исследователей.
В настоящее время в энергетике, авиации и космонавтике, в кораблестроении, теплотехнике, гидротехнике, и ряде других отраслей науки моделирование является основным методом исследований.
Показательным примером стал эксперимент, осуществленный в Институте физики Российской Академии Наук, в ходе которого на модели из фотоупругих материалов было воспроизведено одно из грозных явлений природы – извержение вулканов. Это дало возможность изучить перераспределение напряжения в земной коре и раскрыть некоторые стороны механизма вулканической деятельности.
Наибольший вклад в разработку теории моделирования внесли такие ученые как Кирпичев М.В., Седов Л.И., Павловский Н.Н., Гухман А.А., Михеев М.А., Насонов И.Д., Ньютон, Коши, Рейнольдс, Эйлер, Вебер, Рекле, Грасгоф, Прандль, Фруд, Фурье, Нуссельт и др.
Моделирование как метод исследования имеет целью воспроизведение на модели процесса, подобного процессу в натуре. Этот метод позволяет на уменьшенной или увеличенной модели провести качественные и количественные исследования интересующего нас процесса в натуре, который часто бывает малодоступным или вовсе недоступен для более или менее детального исследования.
Возможно и иное применение метода моделирования, когда образец (машина, комбайн, процесс, явление) еще не существует в натуре. В этом случае исследования проводятся на модели, которая является «прообразом» всех будущих, подобных ей (в геометрическом и физическом смысле) образцов.
Второе назначение метода чаще встречается в производственной деятельности и отвечает, например, задаче изучения вновь запроектированного технологического процесса или какого-либо устройства на его модели.
В науке основной целью моделирования является познание посредством модели объективной действительности этого или иного физического процесса и изучение возможности управления им.
Таким образом, под термином моделирование понимается сам процесс, прием, метод. Модель же является средством познания объективной действительности и под этим термином надо понимать предмет или специальное устройство, искусственно созданное человеком для изучения, интересующего нас объекта.
В зависимости от способа построения и средств модели разделяют на две группы: технические, или материальные, модели и воображаемые или идеальные модели. Между этими группами моделей имеется тесная связь. Прежде чем построить техническую или материальную модель, последняя существует первоначально в голове исследователя как некоторая теоретическая схема, и в этом смысле она является идеальной (воображаемой).
Различают два типа идеальных моделей – модели из чувственно наглядных элементов (упругих шаров, пружин, цилиндров, рычагов и т.д.) и модели из специальных знаковых систем для машинных переходов.
Модели первого типа являются структурными (рис. 1.1), изображающими реологические свойства среды. Они служат для изучения механизма какого-либо сложного физического процесса с входящими в него элементами (изучение физико-механических свойств горных пород).
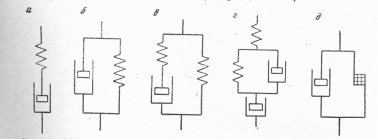
Рис. 1.1. Сложные механические модели физических тел (горных пород):
а – Максвелла; б – Фойта (Кельвина); в – Пойтинга-Томсона (Зенера);
г – Бургарса; д – Шведова-Бингама
Эти комбинации составлены из идеальных сред (рис. 1.2)
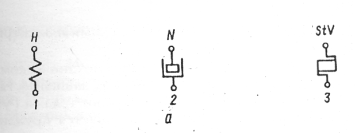
Рис.1.2. Простые идеальные модели физических тел (горных пород)
1 – Гука (упругая модель); 2 – Ньютона (вязкая модель);
3 – Сен-Венона (модель пластичного тела)
Материальные модели по существу являются макетами реальных объектов, в которых воспроизводят те же самые физические процессы или им аналогичные. Для изготовления моделей применяют как материалы натуры, так и материалы физической природы. Такие модели позволяют решить ряд весьма сложных и важных практических задач.
Таким образом, моделирование в познании реальной действительности является звеном, связывающим теорию с практикой: теория – идеальная модель – эксперимент (моделирование) – действительность.
В современных научных исследованиях применяют три вида моделирования: физическое, математическое и функциональное. Наиболее широкое применение в технических науках получили два первых вида моделирования, которые будут нами рассматриваться.
Таким образом, метод моделирования– изучение явлений с помощью моделей – один их основных в современных исследованиях. Основой моделирования является положение о том, что единство природы обнаруживается в поразительной аналогичности дифференциальных уравнений, относящихся к разным областям явлений.
При физическом моделировании физика явлений в объекте, модели и их математические зависимости одинаковы. При математическом моделировании физика явлений может быть различной, а зависимости одинаковыми. Математическое моделирование приобретает особую ценность, когда возникает необходимость изучить особо сложные процессы.
При построении модели свойства и сам объект обычно упрощают, обобщают. Чем ближе модель к оригиналу, тем удачнее она описывает объект, тем эффективнее теоретическое исследование и тем ближе полученные результаты к принятой гипотезе исследования.
Модели могут быть физические, математические, натурные. Физические модели позволяют наглядно представлять протекающие в натуре процессы. С помощью физических моделей можно изучать влияние отдельных параметров на течение физических процессов.
Математические модели позволяют количественно исследовать явления, трудно поддающиеся изучению на физических моделях.
Натурные моделипредставляют собой масштабно изменяемые объекты, позволяющие наиболее полно исследовать процессы, протекающие в натурных условиях.
Стандартных рекомендаций по выбору и построению моделей не существует. Модель должна отображать существенные явления процесса. Мелкие факторы, излишняя детализация, второстепенные явления и т. п. лишь усложняют модель, затрудняют теоретические исследования, делают их громоздкими, нецеленаправленными. Поэтому модель должна быть оптимальной по своей сложности, желательно наглядной, но главное – достаточно адекватной, т.е. описывать закономерности изучаемого явления с требуемой точностью. Естественно, что при построении модели необходимо учитывать особенности исследуемого явления: линейность и нелинейность, детерминированность и случайность, непрерывность и дискретность и др.
Для построения наилучшей модели необходимо иметь глубокие и всесторонние знания не только по теме, смежным наукам, но и хорошо знать практические аспекты исследуемой задачи.
В отдельных случаях модель исследуемого явления может быть ограничена лишь описанием сущности. Так, при изучении укрепления грунтов физико-химическую сущность взаимодействия минералов грунта с вяжущими материалами представить в виде математической модели очень трудно из-за большой сложности процесса. Однако по мере накопления научных данных, постепенно методы их изучения будут заменяться математическими. Это закономерно, поскольку наука может достичь наибольшего совершенства лишь при широком использовании математических методов.
Изучить и проанализировать объект наиболее полно можно лишь при условии, что его модель представлена описанием физической сущности и имеет математический вид. Рассмотрим примеры по составлению моделей.
Анализируя работу грунтов, горных пород, строительных материалов и конструкций, необходимо знать закономерности деформирования их элементов. В зависимости от вида и характера нагрузки, свойств материала элемента могут быть различные условия деформирования, модель которой приведена на рис.1.3. Модель 1, представленная пружиной, характеризует упругие свойства и подчиняется закону Гука – величина деформации пропорциональна прилагаемой нагрузке Р. Такой закон деформирования характерен для твердых упругих тел.
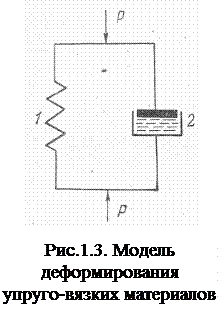 Модель 2, представленная движением поршня в заполненном вязкой жидкостью цилиндра, характеризует вязкие свойства тел. Деформации тел в данном случае происходят медленно, развиваясь во времени, и подчиняются закону Ньютона – сопротивление пропорционально скорости деформирования.
Модель 2, представленная движением поршня в заполненном вязкой жидкостью цилиндра, характеризует вязкие свойства тел. Деформации тел в данном случае происходят медленно, развиваясь во времени, и подчиняются закону Ньютона – сопротивление пропорционально скорости деформирования.
При параллельном соединении двух моделей
1-2 в единое целое имеем модель деформирования упруго-вязкого тела, что характерно для строительных материалов и конструкций. Такое деформирование подчиняется закону Кельвина.
Математическая модель, соответствующая физической модели (см. рис. 3), может быть представлена в виде
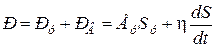 , (1.1)
, (1.1)
где 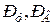 – нагрузки при упругом сжатии пружины в вязком сопротивлении жидкости соответственно;
– нагрузки при упругом сжатии пружины в вязком сопротивлении жидкости соответственно;
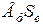 – модуль упругости и относительная деформация пружины;
– модуль упругости и относительная деформация пружины;
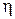 – коэффициент вязкости;
– коэффициент вязкости;
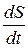 – скорость деформирования.
– скорость деформирования.
Решая (1.1) при 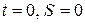 , имеем
, имеем
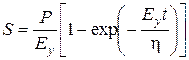 . (1.2)
. (1.2)
Зависимость (1.2) в ряде случаев хорошо согласуется с экспериментом и позволяет изучить законы деформирования упруго-вязких материалов, (грунтов, бетонов, горных пород и др.).
Приведенный пример иллюстрирует процесс познания в соответствии с формулой – от живого созерцания (наблюдение за поведением материала) к абстрактному мышлению (физическая – рис.1.3 и математическая модель уравнения (1.2) и от него к практике. Рассмотренная модель соответствует функциональной зависимости, когда одному значению аргумента соответствует только одно значение функции. Однако в природе встречаются процессы, когда одному значению аргумента соответствует несколько значений функции вследствие действия на явление различных случайных факторов.
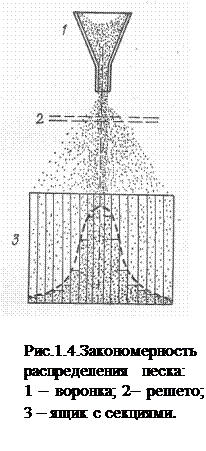 Физическая модель, характеризующая закон вероятностного распределения песка, который вытекает из лейки через решето в ящик с вертикальными секциями, приведена на рис. 1.4.
Физическая модель, характеризующая закон вероятностного распределения песка, который вытекает из лейки через решето в ящик с вертикальными секциями, приведена на рис. 1.4.
Наблюдения показывают, что распределение песка в ящике подчиняется закону нормального распределения:
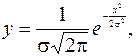 (3)
(3)
где у – ордината, частота распределения песка;
х – абсцисса, номер секции в ящике, отсчитываемой от середины;
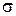 – среднеквадратическое отклонение.
– среднеквадратическое отклонение.
Выражение (1.3) является математической моделью вероятностного процесса физической модели, приведенного на рис.1. 4.
В последнее время широкое распространение получили модели, обеспечивающие оптимизацию технологических процессов и их управления.
В связи с этим, рассмотрим так называемую транспортную задачу.
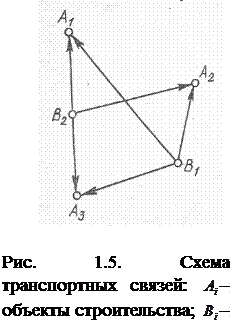 Пусть имеется А1, А2, А3 объектов строительства, потребляющих соответственно а1, а2, а3 щебня (рис. 1.5). В местах В1 и В2 есть притрассовые карьеры с запасами щебня в1 и в2. При этом а1 + а2+ а3 = в1+ в2. Стоимость единицы продукции из карьера В1 на объект А1 равна С11, А2 – С12 на объект А3 – С13. Общее количество щебня xij,, транспортируемое на объект Аi из карьера Bi равно
Пусть имеется А1, А2, А3 объектов строительства, потребляющих соответственно а1, а2, а3 щебня (рис. 1.5). В местах В1 и В2 есть притрассовые карьеры с запасами щебня в1 и в2. При этом а1 + а2+ а3 = в1+ в2. Стоимость единицы продукции из карьера В1 на объект А1 равна С11, А2 – С12 на объект А3 – С13. Общее количество щебня xij,, транспортируемое на объект Аi из карьера Bi равно
х11 + х21 = а1;
х12 + х22 = а2;
х13 + х23 = а3; (1.4)
х11 + х12 + х13 = в1;
х21 + х22 + х23 = в2,
где а1, а2, а3 – потребности щебня на объектах.
В системе (1.4) первое уравнение означает количество щебня, транспортируемое на объект А1 из карьеров В1 и В2; второе – на объект А2. Последнее уравнение – количество щебня, доставляемое на объекты А1, А2 , А3 из карьера В2.
Все исходные данные сведены в матрицу условия задачи (табл. 1.1).
Таблица 1.1
| Карьеры | Объекты | Запасы | ||
| А1 | А2 | А3 | ||
| В1 | С11 х11 | С12 х12 | С13 х13 | в1 |
| В2 | С21 х21 | С22 х22 | С23 х23 | в2 |
| Общая потребность | а1 | а2 | а3 |
Требуется определить наиболее выгодный (экономичный вариант перевозки щебня.
В этом случае численными методами с помощью линейного программирования и ЭВМ находят функцию, которая удовлетворяет условию
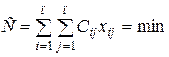 . (1.5)
. (1.5)
Уравнение (1.5) является математической моделью, позволяющей оптимизировать транспортный процесс. Физическая модель изображена на рис.1.5.
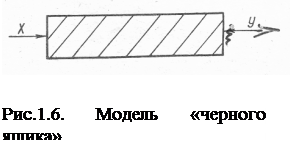 В последнее время большой интерес вызвала кибернетическая модель «черного ящика» (рис.1.6), описывающая систему, структура которой неизвестна и недоступна для наблюдения. Известны лишь «Х» (ввод) и «У» (вывод). Задача сводится к подбору таких значений Х, которые обеспечили бы соответствующие (в большинстве случаев) оптимальные значения У. Статистическим путем находят модели исследуемого процесса. Во многих случаях для построения таких моделей целесообразно использовать метод математического планирования эксперимента.
В последнее время большой интерес вызвала кибернетическая модель «черного ящика» (рис.1.6), описывающая систему, структура которой неизвестна и недоступна для наблюдения. Известны лишь «Х» (ввод) и «У» (вывод). Задача сводится к подбору таких значений Х, которые обеспечили бы соответствующие (в большинстве случаев) оптимальные значения У. Статистическим путем находят модели исследуемого процесса. Во многих случаях для построения таких моделей целесообразно использовать метод математического планирования эксперимента.
 В теоретических исследованиях применяют модели-аналоги и модели-подобия. Основываясь на подобии или аналогии объектов, процессов и т.п., изучают экспериментально теоретическим путем явления на модели, а затем с помощью соответствующего математического аппарата устанавливают закономерности в натуре.
В теоретических исследованиях применяют модели-аналоги и модели-подобия. Основываясь на подобии или аналогии объектов, процессов и т.п., изучают экспериментально теоретическим путем явления на модели, а затем с помощью соответствующего математического аппарата устанавливают закономерности в натуре.
Электрическая модель-аналог для изучения напряженно-деформированного состояния балки на двух опорах приведена на рис. 1.7.
Реакции на опорах балки вычисляются по формулам 
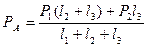 ;
;
(1.6)
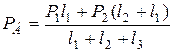 .
.
Силу тока на входе и выходе электрической цепи вычисляют аналогично:

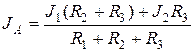 ,
,
(1.7)
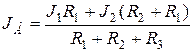 .
.
Таким образом, меняя силу тока I1, I2 и сопротивление R1, можно изучать реакцию опор балки в зависимости от величины Р1 и Р2.
Модели подобия используют давно. Например, нет необходимости теоретически вычислять или непосредственно измерять величину Н Останкинской башни в Москве. Для этой цели достаточно использовать простейшую модель – треугольник и с помощью теоремы о подобии треугольников путем измерения расстояния к башне Z определить ее высоту по формуле
H=h·Kp , (1.8)
где Kр – критерий подобия, равный Kр = Z : l ( l – сторона треугольника).
Аналогичный прием широко используют и при исследовании процессов, но критерий подобия и уравнения в этом случае значительно сложнее. Анализ многообразных физических моделей изучаемых процессов исследуется математическими методами, которые могут быть разделены на такие основные группы:
Аналитические методыисследования (элементарная математика, дифференциальные и интегральные уравнения, вариационное исчисление и другие разделы высшей математики), используемые для изучения непрерывных детерминированных процессов.
Методы математического анализа с использованием эксперимента (метод аналогий, теория подобия, метод размерностей) и др.
Вероятностно-статистические методы исследования (статистика и теория вероятностей, дисперсионный и корреляционный анализы, теория надежности, метод Монте-Карло и др.) для изучения случайных процессов – дискретных и непрерывных.
Дальнейшее развитие горной науки настоятельно требует наряду с проведением теоретических исследований все более широкого применения методов моделирования и, главным образом, дальнейшего развития методов математического моделирования, опережающего по сравнению с развитием физического моделирования и натурного экспериментирования.
Дата добавления: 2017-10-04; просмотров: 1658;











