Подобие физических полей
Подобие стационарных полей. Стационарным полем любой физической величины j называется совокупность значений этой величины во всех точках изучаемого пространства или объема. Стационарное поле не изменяется во времени. Обычно математическая формулировка определяется уравнением
j = f(x,y,z) (2.15)
Однако такой прием аналитического описания поля физической переменной j является не совсем правильным. Действительно, под значением j понимают любую физическую переменную (температуру, скорость, плотность, концентрацию и т.д.) Согласно правилу Фурье размерность правой части должна соответствовать размерности левой. Поэтому под знак функции f кроме координат x,y,z должны быть введены еще некоторые физические параметры 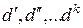 с различными размерностями, с тем, чтобы размерности правой и левой части уравнения (22) были одинаковы. Кроме физических параметров под знак функции следует ввести геометрические параметры
с различными размерностями, с тем, чтобы размерности правой и левой части уравнения (22) были одинаковы. Кроме физических параметров под знак функции следует ввести геометрические параметры 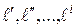 .
.
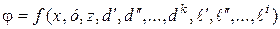 (2.16)
(2.16)
Допустим, что имеется две геометрически подобные системы, у которых поля физических переменных j1 иj2 имеют одинаковую размерность, т.е.

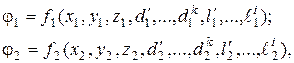 (2.17)
(2.17)
где 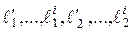 – сходственные геометрические параметры подобных систем;
– сходственные геометрические параметры подобных систем;
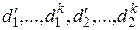 – соответственно, физические одноименные параметры (имеют одинаковую размерность).
– соответственно, физические одноименные параметры (имеют одинаковую размерность).
Пусть j1 иj2 разделяются в своих системах так, что любой паре сходственных точек, т.е. при равенстве отношений
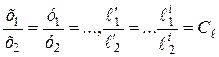 , (2.18)
, (2.18)
имеет место равенство отношений
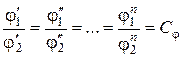 , (2.19)
, (2.19)
При этом в общем случае 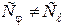 .
.
Такие физические поля называются подобными стационарными. В подобных физических полях для сходственных одноименных физических параметров имеют место равенства
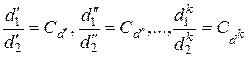 (2.20)
(2.20)
причем, в общем случае 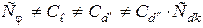 .
.
Таким образом, подобные стационарные физические поля с формально-геометрической точки зрения являются аффинными, т.к. их совмещение может быть осуществлено путем неравномерной деформации, т.е. если в качестве масштабов выбрать сходственные величины (геометрические, физические), то в сходственных точках подобных стационарных полей безразмерные координаты и безразмерные физические переменные соответственно равны.
Действительно, введя в равенство (2.18) и (2.19) масштабные преобразования
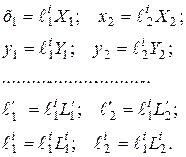 (2.21)
(2.21)
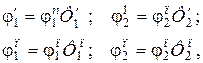 (2.22)
(2.22)
получим после сокращения на 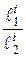 и
и 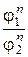
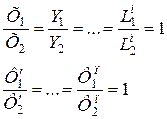 (2.23)
(2.23)
или 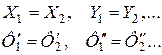 (2.24)
(2.24)
Дополним преобразования (2.21) и (2.22) преобразованиями физических параметров
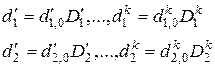 ý (2.25)
ý (2.25)
где 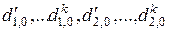 – масштабы физических параметров
– масштабы физических параметров 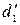 ,… и сходственные масштабы одноименных физических параметров
,… и сходственные масштабы одноименных физических параметров 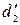 ,…
,…
Докажем равенство сходственных безразмерных параметров.
Введя масштабные преобразования (2.25) в выражение (2.20)
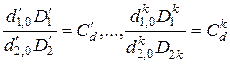 (2.26)
(2.26)
Но из выражения (2.20)

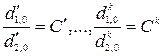 , т.е.
, т.е. 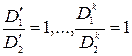
или 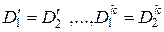 , что и требовалось доказать.
, что и требовалось доказать.
Подобие нестационарных полей. Нестационарным полем любой физической переменной y называется совокупность мгновенных их значений этой переменной во всех точках изучаемого пространства или объема. Значения переменной y изменяется во времени. Математически эта формулировка описывается уравнением
y = f(x, y, z, t), (2.27)
где t – время.
Исходя из предыдущих рассуждений о равенстве левой и правой части уравнения (34), запишем
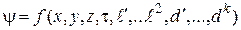 . (2.28)
. (2.28)
Допустим, в двух геометрических подобных системах поля имеют одинаковую размерность и заданы уравнениями
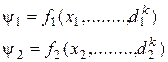
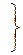 , (2.29)
, (2.29)
где t1, t2 – сходственные моменты времени.
Два промежутка времени t1 и t2 называются сходственными, если они имеют общее начало отсчета и связаны преобразованием подобия вида
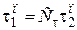 . (2.30)
. (2.30)
Нестационарные поля y1 и y2 – подобны, если в каждой паре сходственных точек, т.е. при равенствах
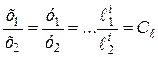 , ,
|
и в сходственные моменты времени, т.е. при равенствах отрезков времени для первой и второй систем
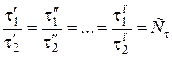 (2.31)
(2.31)
будет иметь место равенство
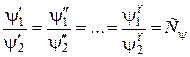 . (2.32)
. (2.32)
В общем случае множители подобия 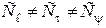 .
.
Следовательно, нестационарные физические поля также являются аффинными системами, и совмещение этих полей может быть достигнуто при неравномерной деформации. Таким образом, нестационарные физические поля обладают теми же свойствами, что и аффинные системы.
Так же как и для стационарного поля, в данном случае с помощью масштабных преобразований можно доказать, что у подобных нестационарных физических полей безразмерные одноименные координаты сходственных точек и безразмерные сходственные моменты времени равны, т.е.
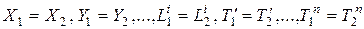 . (2.33)
. (2.33)
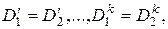 (2.34)
(2.34)
то 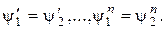 (2.35)
(2.35)
При этом в общем случае 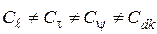 .
.
В качестве простейшего примера рассмотрим скоростное поле течения жидкости в трубе при ламинарном режиме течения. Из гидродинамики известно, что это поле описывается уравнением
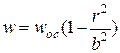 , (а)
, (а)
| где | w | – | скорость в любой точке, находящейся на расстоянии r от оси трубы; |
| wос | – | скорость на оси трубы; | |
| b | – | радиус трубы. |
Допустим, имеем две трубы различных диаметров, тогда уравнения скоростных полей для них можно записать в виде
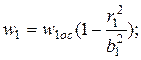 (б)
(б)
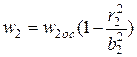 . (в)
. (в)
Для приведения уравнений (б) и (в) к безразмерному виду введем масштабные преобразования
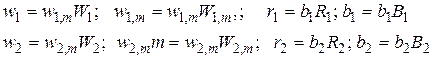
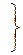 . (г)
. (г)
Из этих соотношений
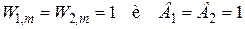 .
.
Введя масштабные преобразования (г) в уравнения (б) и (в), получим
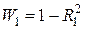 ; (д)
; (д)
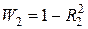 . (е)
. (е)
Нетрудно видеть, что при R1 = R2 или 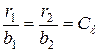 , т.е. в геометрически сходственных точках, должны быть W1 = W2 или
, т.е. в геометрически сходственных точках, должны быть W1 = W2 или
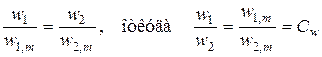
Следовательно, поля скоростей в обеих трубах подобны.
Дата добавления: 2017-10-04; просмотров: 1558;











