Кривые и поверхности второго порядка

Окружность. Определение. Окружностью называется множество всех точек плоскости, расстояние каждой из которых от одной точки плоскости, называемой центром, есть величина постоянная.

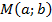Пусть - центр окружности, 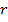- её радиус, 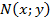- произвольная точка окружности (рис.29). Тогда по формуле (2) имеем:

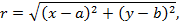
или

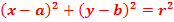(29)

Уравнение (29) называется нормальным уравнением окружности.

Если точка 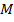совпадает с началом координат, т.е. 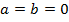, то уравнение окружности примет вид: 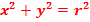. (29а)

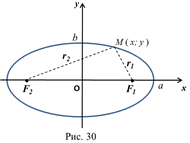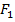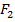Эллипс. Определение. Эллипс есть множество всех точек плоскости, сумма расстояний каждой из которых от двух данных точек и , называемых фокусами, есть величина постоянная, обозначаемая через .

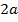Расстояние 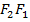между фокусами называется фокусным расстоянием и обозначается через 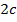, т.е. 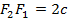. Если систему координат построить таким образом, чтобы ось абсцисс проходила через точк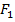и и 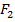, причём 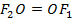, то фокусы будут иметь координаты 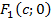и .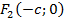

Пусть 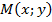- произвольная точка эллипса. Тогда по определению эллипса 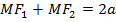, причём 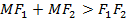, т.е. 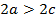, или 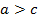. По формуле (2) имеем:

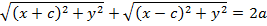
После преобразований и соответствующих замен последнего равенства, получим:

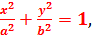(30)

где .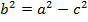

Если центр эллипса находится в точке 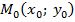, то уравнение эллипса запишется:

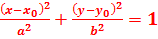(30а)

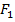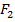Гипербола. Определение. Гипербола есть множество всех точек плоскости, разность расстояний которых от двух данных точек и , называемых фокусами, есть величина постоянная, обозначаемая через .

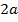Расстояние 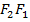между фокусами называется фокусным расстоянием и обозначается через 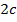, т.е. 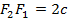. Если систему координат построить таким образом, чтобы ось абсцисс проходила через точк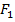и и 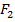, причём 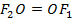, то фокусы будут иметь координаты 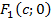и .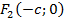

Пусть 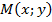- произвольная точка эллипса. Тогда по определению гиперболы 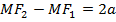, причём 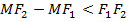, т.е. 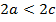, или 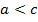. По формуле (2) имеем:

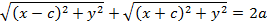
После преобразований и соответствующих замен последнего равенства, получим:

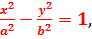(31)

где .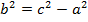

Если центр гиперболы находится в точке 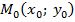, то уравнение гиперболы запишется:

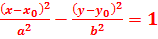(31а)

Парабола. Определение. Парабола есть множество всех точек плоскости, находящихся на одинаковом расстоянии от одной неподвижной точки 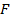плоскости, называемой фокусом, и от одной неподвижной прямой 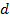, называемой директрисой.

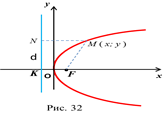Систему координат построим так, чтобы ось абсцисс проходила через точку 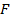, , 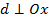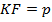и 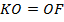. Тогда фокус 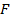имеет координаты 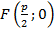. Пусть 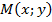- произвольная точка параболы. Тогда по определению параболы 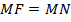. Если учесть, что точка 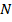имеет координаты 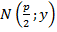, то последнее условие запишется так:

.

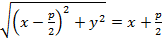После преобразований получим уравнение параболы:

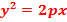(32)

Если вершина параболы находится в точке 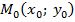, то уравнение параболы запишется:

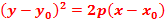(32а)

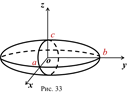
Эллипсоид. Определение. Эллипсоидом называется поверхность, каноническое уравнение которой имеет вид 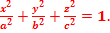(рис. 33)

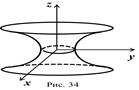
Однополостный гиперболоид. Определение. Однополостным гиперболоидом называется поверхность, простейшее уравнение которой имеет вид 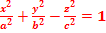. (рис. 34)

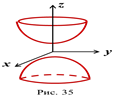
Двухполостный гиперболоид. Определение. Двухполостным гиперболоидом называется поверхность, простейшее уравнение которой имеет вид 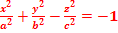. (рис.35)

Эллиптический параболоид. Определение. Эллиптическим параболоидом называется поверхность, простейшее уравнение которой имеет вид

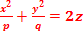. (рис.36)

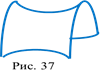Гиперболический параболоид. Определение. Гиперболическим параболоидом называется поверхность, простейшее уравнение которой имеет вид

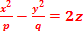(рис. 37)

Эллиптический цилиндр. Определение. Эллиптическим цилиндром называется поверхность, простейшее уравнение которой имеет вид

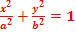(рис. 38)

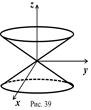
Конус второго порядка. Определение. Конусом второго порядка называется поверхность, простейшее уравнение которой имеет вид

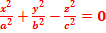(рис. 38)

Параболический цилиндр. Определение. Параболическим цилиндром называется поверхность, простейшее уравнение которой имеет вид 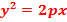(рис. 40)

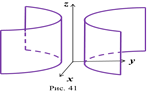
Гиперболический цилиндр. Определение. Гиперболическим цилиндром называется поверхность, простейшее уравнение которой имеет вид 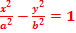(рис. 41)