Решение некоторых задач из аналитической геометрии
Задача 1. Составить уравнение плоскости, которая имеет нормальный вектор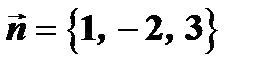 
и проходит через точку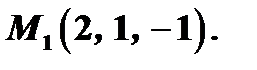 
Запишем уравнение плоскости в общем виде 
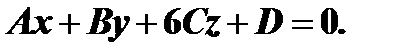По условию 
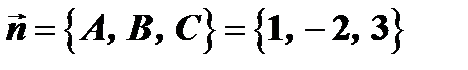. Следовательно, уравнение плоскости примет вид 
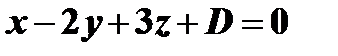. Для определения 
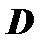воспользуемся условием того, что плоскость проходит через точку 
: 
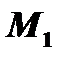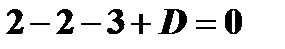, откуда 
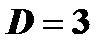. Подставив в уравнение плоскости полученное значение 
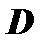, имеем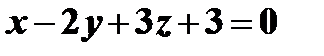 
Задача 2. Найти уравнение плоскости, проходящей через точк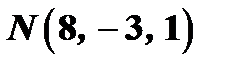и 
и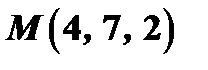 
и перпендикулярной к плоскости 
.
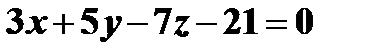Уравнение плоскости, проходящей через точку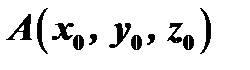 
имеет вид: 
.
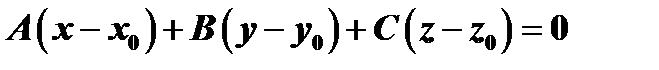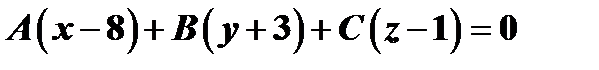- проходит через точку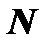 
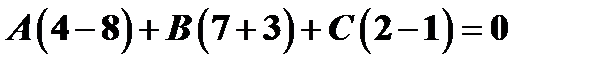- проходит через точку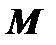 
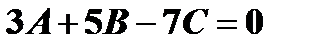-условие перпендикулярности двух плоскостей
В итоге получим однородную систему линейных уравний относительно неизвестных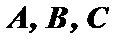 
:
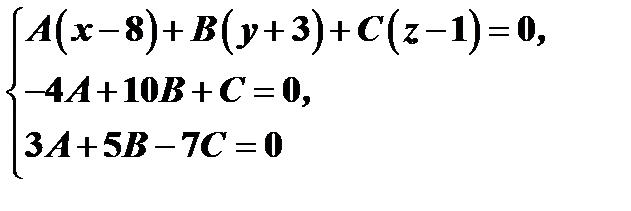
Как известно, однородная система имеет ненулевое решение, если определитель, составленный из коэффициентов системы равен нулю, т.е.
,
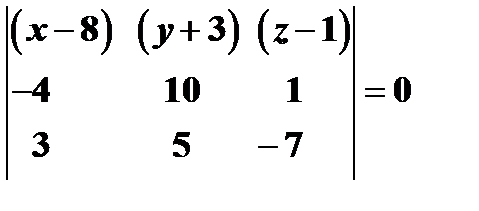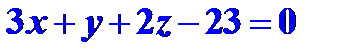откуда .
Задача 3. Провести плоскость через точку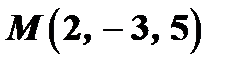 
, параллельную плоскости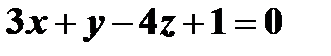 
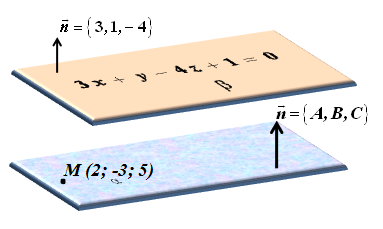Уравнение плоскости, проходящей через точку 
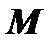, имеет вид: 
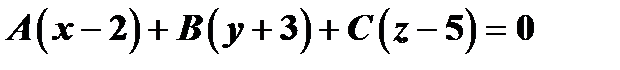. Так как плоскости параллельны, то нормальные векторы также параллельны, т.е. 
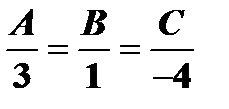, откуда 
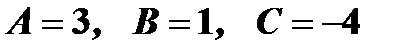. Подставив значения 
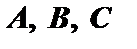в уравнение плоскости, получим 
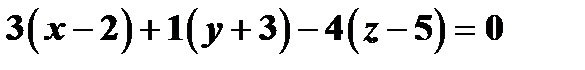, или, после приведения подобных членов 
.
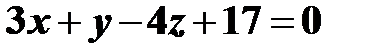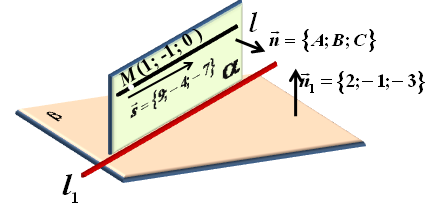Задача 4. Найти уравнения проекции прямой 
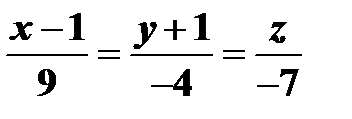на плоскость 
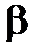, заданную уравнением 
.
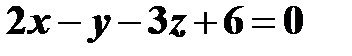Найти уравнения проекции прямой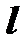 
на плоскость 
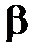равносильно найти линию пересечения плоскост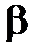и 
и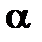 
, проходящую через прямую 
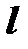и перпендикулярную 
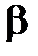. Т.к. точка 
, то 
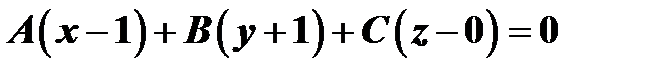и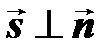 
, имеем 
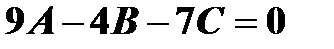.Кроме того, 
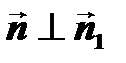, следовательно, 
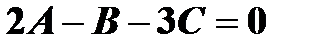. В итоге получим систему уравнений
.
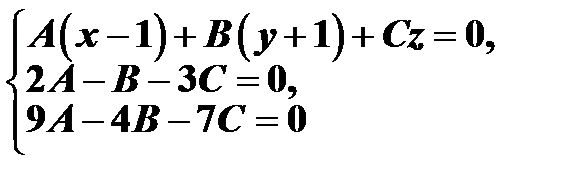Эта система имеет ненулевое решение, если
.
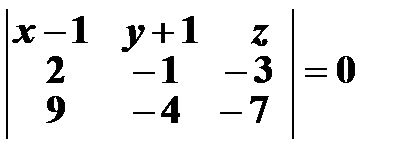Раскрывая определитель, получим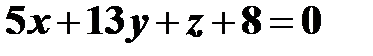 
. Следовательно, уравнения прямой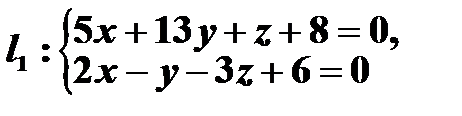 
Задача 5. Написать уравнение плоскости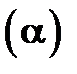 
, проходящей через точку 
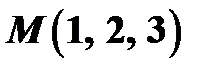и перпендикулярной к плоскостям 
.
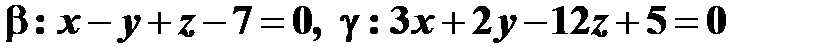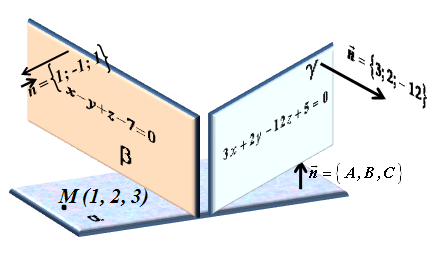
- проходит черз т. М
|
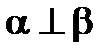
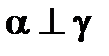
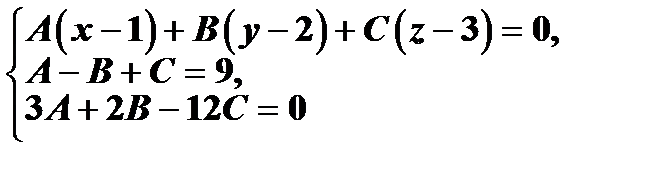
Как в задаче 2:
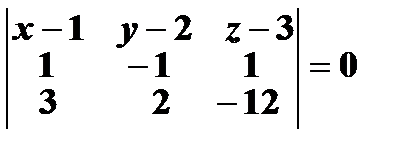
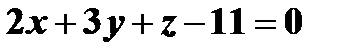
Задача 6. Перейти от общих уравнений прямо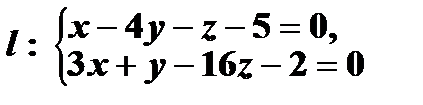 
к её каноническому виду.
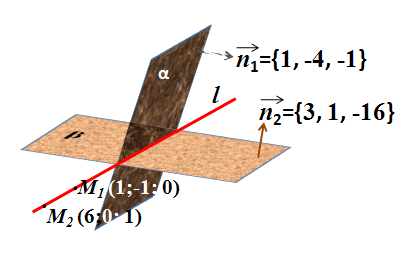Каконические уравнения прямой имеет вид 
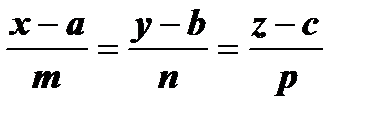, но для решения данной задачи мы воспользуемся уравнениями прямой по двум точкам 
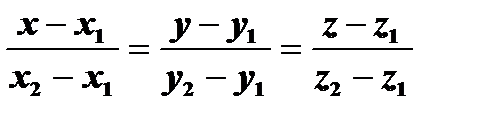, где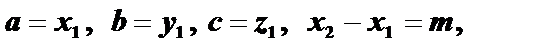 
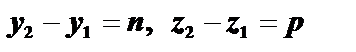. Для определения этих двух точек поступают следующим образом:
1. Пусть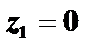 
, тогда +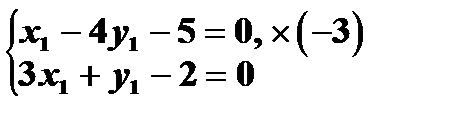 
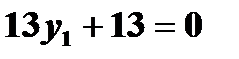
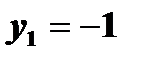
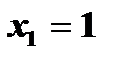
2. Пусть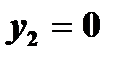 
, тогда +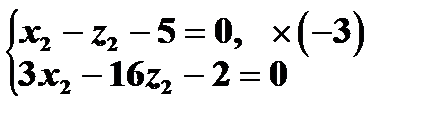 
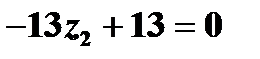
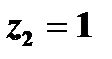
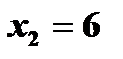
Подставим полученные значения в уравнение, получим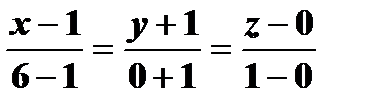 
, откуда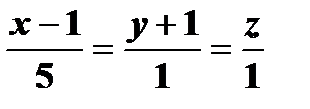 
Использованная литература:
1. Н.В. Богомолов, П.И. Самойленко, Математика
2. Н.В. Богомолов, Практические занятия по математике
3. А.Н. Рублёв, Курс линейной алгебры и аналитической геометрии
4. Д.И. Клетеник, Сборник задач по аналитической геометрии
5. И.И. Привалов, Аналитическая геометрия
6. С.И. Фролов и др., Курс высшей математики
7. О.Н. Цубербиллер, Задачи и упражнения по аналитической геометрии
8. Э.С. Маркович, Курс высшей математики с элементами теории вероятностей и математической статистики
9. Н.А. Сахарников, Высшая математика
10. Н.С. Пискунов, Дифференциальное и интегральное исчисления, ч.1
11. Г.Н. Берман, Сборник задач по курсу математического анализа
12. П.Е. Дюбюк и др., Сборник задач по курсу высшей математик
Дата добавления: 2017-10-04; просмотров: 2179;
Поиск по сайту
Узнать еще
Публикации по технике и механике
Публикации по биологии
Публикации по информатике
Публикации по строительству
Публикации по физике
Публикации по химии
Публикации по электронике
Публикации по искусству
Публикации по истории
Публикации по медицине
