Определители третьего порядка
Определителем третьего порядка называется число, определяемое равенством 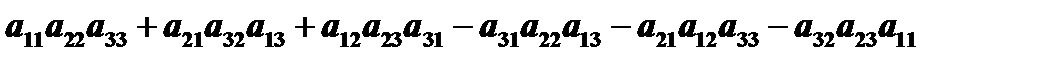 и обозначается
и обозначается
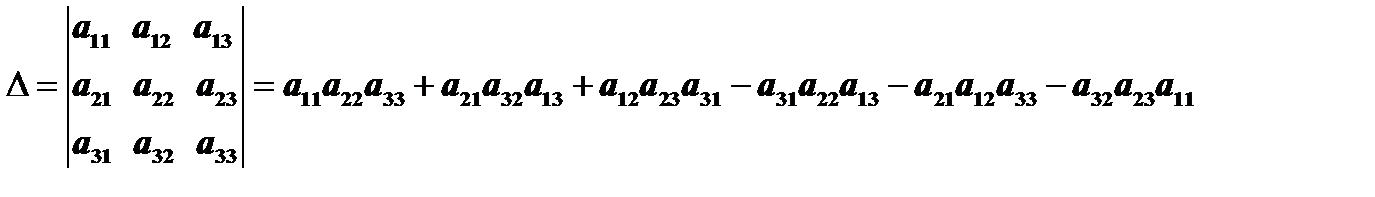
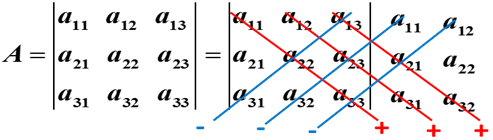
Схема вычисления определителя третьего порядка

Если из определителя 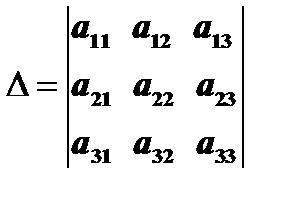 вычеркнуть одну строку и один столбец, на пересечении которых стоит некоторый элемент, то получится определитель второго порядка, который называется миноромопределителя
вычеркнуть одну строку и один столбец, на пересечении которых стоит некоторый элемент, то получится определитель второго порядка, который называется миноромопределителя  , соответствующим этому элементу. Так, например, если из определителя
, соответствующим этому элементу. Так, например, если из определителя 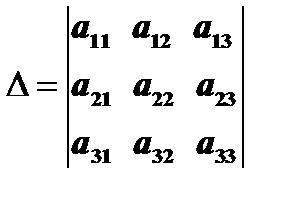 вычеркнуть вторую строку и третий столбец
вычеркнуть вторую строку и третий столбец 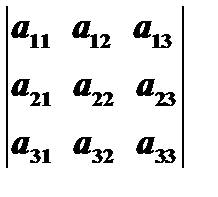 , то минором элемента
, то минором элемента 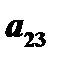 будет определитель второго порядка
будет определитель второго порядка 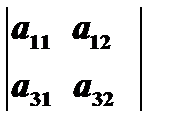 и обозначается
и обозначается 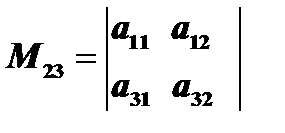 . Условимся называть алгебраическим дополнением
. Условимся называть алгебраическим дополнением 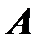 некоторого элемента
некоторого элемента 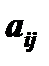 соответствующий ему минор, взятый со знаком плюс или минус, смотря по тому, будет ли сумма номеров строки и столбца, которым принадлежит данный элемент, четным или нечетным числом, т.е.
соответствующий ему минор, взятый со знаком плюс или минус, смотря по тому, будет ли сумма номеров строки и столбца, которым принадлежит данный элемент, четным или нечетным числом, т.е.
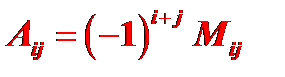
Вернемся к определителю третьего порядка:
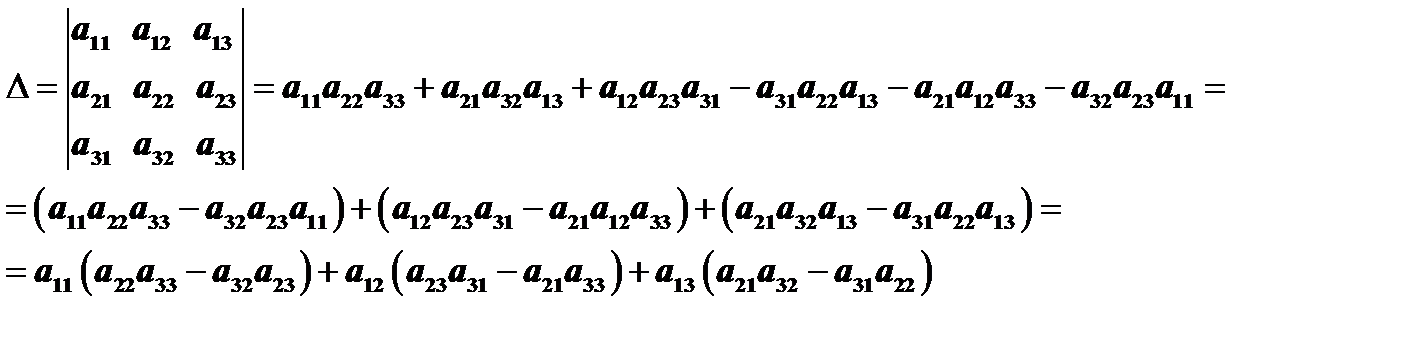
Заметим, что в скобках стоят алгебраические дополнения элементов 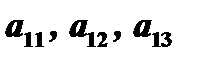 , соответственно. Поэтому определитель можно переписать в виде
, соответственно. Поэтому определитель можно переписать в виде 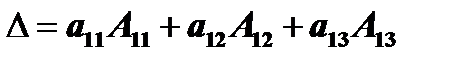 . О последнем выражении говорят, что определитель разложен по элементам первой строки. Легко проверить, что аналогичная формула имеет место и по отношению к любому столбцу, а значит, и к любой строке.
. О последнем выражении говорят, что определитель разложен по элементам первой строки. Легко проверить, что аналогичная формула имеет место и по отношению к любому столбцу, а значит, и к любой строке.
Основные свойства определителей:
1. При замене строк столбцами величина определителя не меняется.
2. При перестановке двух столбцов (или строк) определитель меняет лишь знак.
3. Определитель с двумя одинаковыми столбцами (или строками) равен нулю.
4. Сумма произведений элементов некоторого ряда (столбца или строки) на алгебраические дополнения этих элементов равна определителю, а сумма произведений элементов некоторого ряда (столбца или строки) на алгебраические дополнения соответствующих элементов параллельного ряда (столбца или строки) равна нулю.
5. Множитель, общий элементам некоторого ряда (столбца или строки), можно выносить за знак определителя.
6. Определитель равен нулю, если все элементы некоторого его ряда (столбца или строки) равны нулю.
7. Если элементы некоторого ряда (столбца или строки) представляют собой сумму двух слагаемых, то определитель может быть представлен в виде суммы двух определителей, у которых элементы рассматриваемого ряда равны соответственным слагаемым.
8. Величина определителя не изменится, если к элементам некоторого ряда (столб- ца или строки) прибавить (или от них вычесть) элементы параллельного ряда (столбца или строки), предварительно умножив эти последние на один и тот же произвольный множитель.
Определителем 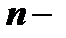 го порядка называется сумма произведений элементов какого-нибудь столбца (или строки) матрицы на их алгебраические дополнения.
го порядка называется сумма произведений элементов какого-нибудь столбца (или строки) матрицы на их алгебраические дополнения.
М А Т Р И Ц Ы
Определение. Матрицей называется совокупность  чисел, расположенных в виде прямоугольной таблицы, содержащей
чисел, расположенных в виде прямоугольной таблицы, содержащей 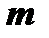 строк и
строк и 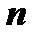 столбцов и записывается в виде
столбцов и записывается в виде
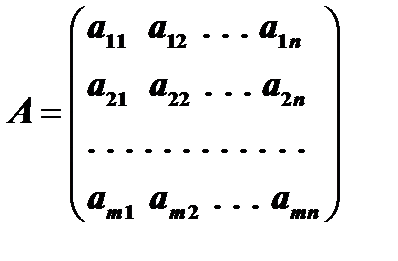 ,
, 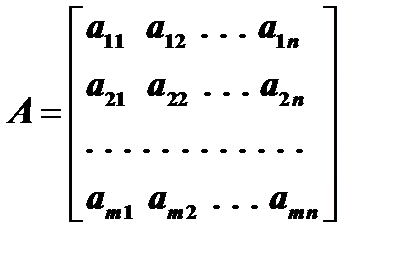 ,
, 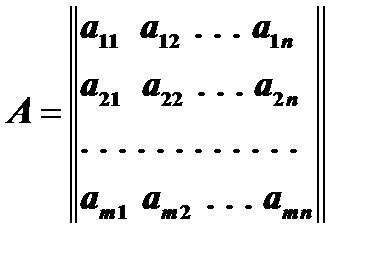 (1) или сокращенно
(1) или сокращенно 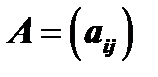 ,
, 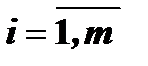 ,
, 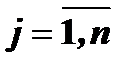 .
.
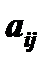 - элемент матрицы,
- элемент матрицы, 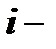 номер строки,
номер строки, 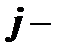 номер столбца.
номер столбца.
Две матрицы, имеющие одинаковое число строк и одинаковое число столбцов, называются матрицами одинакового типа. Для матриц одинакового типа устанавливается понятие их равенства: две матрицы считаются равными, если попарно равны их элементы, стоящие на одинаковых местах.
Матрица, состоящая из одной строки или одного столбца, называется соответственно вектор-строкой или вектор-столбцом. Матрица типа 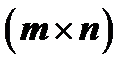 , все элементы которой равны нулю, называется нулевой матрицей и обозначается через
, все элементы которой равны нулю, называется нулевой матрицей и обозначается через 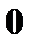 . Матрица типа
. Матрица типа 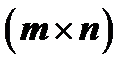 обычно называют прямоугольной.
обычно называют прямоугольной.
Если число строк равно числу столбцов, то такую матрицу называют квадратной. Совокупность элементов квадратной матрицы, расположенных на отрезке, соединяющем левый верхний угол с правым нижним, называют главной диагональю, а на отрезке, соединяющем правый верхний угол с левым нижним, - побочной диагональю матрицы. Квадратные матрицы, у которых отличны от нуля лишь элементы главной диагонали, называются диагональнымиматрицами. Квадратная матрица называется треугольной, если все элементы, стоящие выше (или ниже) главной диагонали, равны нулю. Единичной матрицей называется диагональная матрица, у которой каждый элемент, находящийся на главной диагонали, равен единице и обозначается через 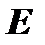 .
.
Транспонированной называется матрица 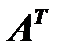 , получаемая из данной матрицы
, получаемая из данной матрицы 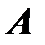 вида (1) путем замены строк столбцами, таким образом,
вида (1) путем замены строк столбцами, таким образом,
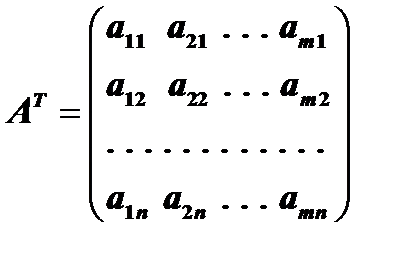
Дата добавления: 2017-10-04; просмотров: 2384;











